Реферат: Численное решение краевых задач для двумерного уравнения колебания

Пример 4 . Задачу (1.20) аппроксимируем схемой с весом

(1.25)

Отсюда имеем

Условие (1.22) будет выполнено, если

т.е.

Отсюда получаем

Схема абсолютно устойчива при

и

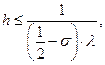
т.е. схема (7.25) условно устойчива при [4].

1.6. Аппроксимация и сходимость

Для того, чтобы выяснить, с какой точностью приблизили функцию u=u(x) с помощью функции у(х), мы должны их сравнить. Пусть u^h значение функции u(х) на сеточной области , т.е. u^h H_h .

Рассмотрим погрешность решения разностной схемы (1.14), (1.15), которая аппроксимирует на сетке дифференциальную задачу (1.12), (1.13).

Введем функцию погрешности решения

z_h =y_h -u^h ,

где y_h - решение схемы (1.14), (1.15), u^h - решение задачи (1.12), (1.13) на сетке . Подставив y_h = z_h + u^h в линейную задачу (1.14), (1.15), полу­чим для z_h задачу того же вида, что и (1.14), (1.15):

(1.26)

(1.27)

где (1.28)

Функции (1.28) называются погрешностью аппроксимации задачи (1.12), (1.13), схемой (1.14), (1.15) на решении задачи (1.12), (1.13).

Будем говорить, что решение разностной схемы (1.14), (1.15) сходится к решению задачи (1.12), (1.13), если

при

Разностная схема сходится со скоростью O(h^h ) или имеет n-ый порядок точности, если при достаточно малом hh₀ выполняется неравенство

где М>0, не зависит от h, n>0.