Реферат: Численное решение краевых задач для двумерного уравнения колебания

Основной задачей выпускной работы является:

- рассмотреть методы расщепления для двумерного уравнения колебания;

В выпускной работе четыре параграфа. В первом параграфе дана теоретическая часть, в котором отражены основные понятия из теории разностных схем.

Второй параграф выпускной работы посвящен основным понятиям и истории вопроса экономичных разностных схем.

Третий и четвертый параграф содержит материалы собственных исследований по методам расщепления для двумерного уравнения колебания.

Выпускная работа состоит из введения, четырех параграфов (разностных методов решения задач для дифференциальных уравнений, основных понятий и истории вопроса элементарных разностных схем, схемы расщепления с последовательным переходом, схемы расщепления с параллельным переходом), заключения и списка использованной литературы.

§1. Разностные методы решения задач

для дифференциальных уравнений

(основные понятия теории разностных схем)

Теория разностных схем является самостоятельным разделом вы­числительной математики, где изучаются методы приближенного решения дифференциальных уравнений путем замены их конечно-разностными уравнениями (разностными схемами).

Пусть имеем дифференциальную задачу, записанную в символичес­кой форме:

Lu(x)=f(x), (1.1)

где хG, f - заданная функция, L - линейный дифференциальный опе­ратор. Предполагается, что дополнительные условия дифференциаль­ного уравнения (граничные и начальные) учтены оператором L и пра­вой частью f.

Рассмотрим примеры. Пусть имеем дифференциальную задачу

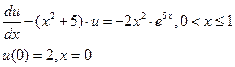
которую запишем в виде (1.1):

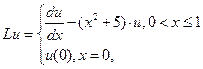
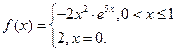
Задача

запишется в виде (1.1), если положить

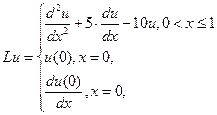
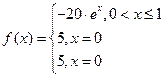
Для записи в виде (1.1) задачи

с краевыми условиями на обеих концах отрезка надо положить:

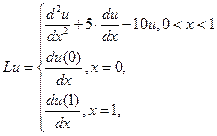
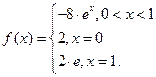
Конечно-разностный метод (метод сеток) - один из мощных доста­точно универсальных методов современной вычислительной матема­тики. Этот метод относится к классу машинных методов решения широкого круга задач для дифференциальных уравнений [4].