Реферат: Численные методы

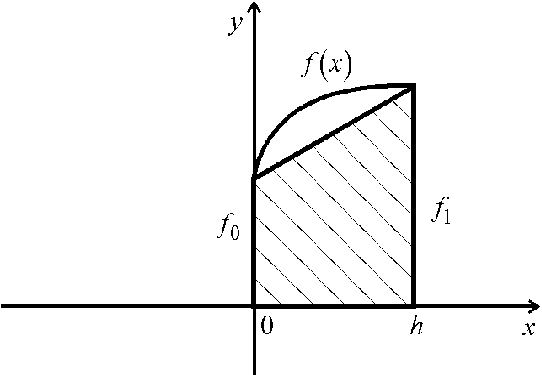
Найдем остаточный член, т.е. погрешность формулы (7). Выразим і где - функция (4), по формуле Тейлора с остаточным членом в интегральной форме :

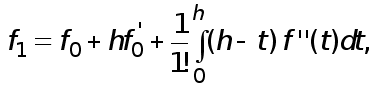(8)

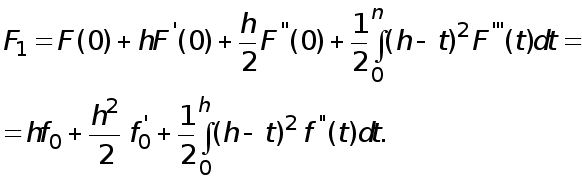(9)

Согласно (8) имеем

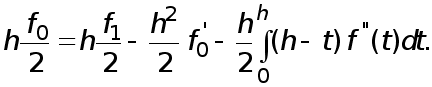(10)

Отделив в правой части (9) слагаемое и заменив его выражением (10), с учетом того, что 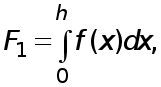находим

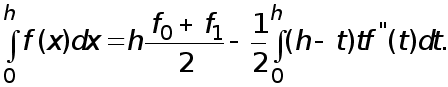
Преобразуем теперь второе слагаемое в правой части, используя обобщенную теорему о среднем.

* Формула Тейлора с остаточным членом в интегральной форме

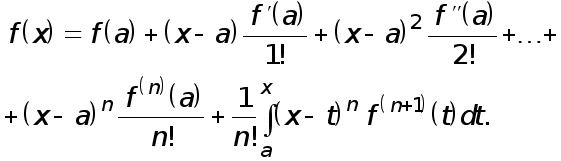
Теорема 1 (обобщенная теорема о среднем). Пусть причем на Тогда существует такая точка что

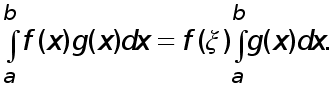
Доказательство. Положим

(11)

Тогд, так как то

и, следовательно,

Если то и в качестве можн взять любую точку из

Если то вытекает существование такого числа с, удовлетворяющего неравенствам ( для этого делим все части на ):

(12)

что

(13)

По теореме о промежуточных значениях непрерывной функции в силу (11) , (12) найдется точка , в которой что вместе с равенством (13) доказывает теорему .

Теперь, так как то по доказанной теоремою

где - некоторая точка . Подставляя полученное в , приходим к формуле трапеций с остаточным членом :