Реферат: Численные методы

Отсюда,учитывая выражения для функций получаем при уравнения

Обозначая перепишем эти уравнения в виде

(2)

Условия непрерывности первой производной

приводят к уравнениям

(3)

Из условий непрерывности второй производной получаем уравнения

. (4)

Объединяя (2) -(4) , получим систему уравнений относительно неизвестных

Два недостающих условия получают, задавая те или иные граничные условия для Предположим, например, что функция удовлетворяет условиям Тогда естественно требовать, чтобы Отсюда получаем

т.е.

Заметим, что условие совпадает с уравнением (4) при . Таким образом, приходим к замкнутой системе уравнений для определения коэффициентов кубического сплайна:

Убедимся в том, что эта система имеет единственное решение. Исключим из (5)- (7) переменные и получим систему, содержащую только Для этого рассмотрим два соседних уравнения (7) :

и вычтем второе уравнение из первого. Тогда получим

Подставляя найденное выражение для в правую часть уравнения (6), получим

(8)

Далее, из уравнения (5) получаем

И подставляя эти выражения в (8) , приходим к уравнению

Окончательно для определения коэффициентов получаем систему уравнений

(9)

В силу диагонального преобладания система (9) имеет единственное решение. Так как матрица системы трехдиагональная, решение можно найти методом прогонки. По найденным коэффициентам коэффициенты і определяются с помощь явных формул

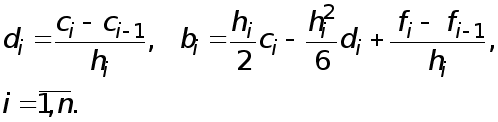(10)

Таким образом, доказано, что существует единственный кубический сплайн, определяемый условиями а)-в) и граничными условиями Заметим , что можно рассматривать и другие граничные условия.

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ.