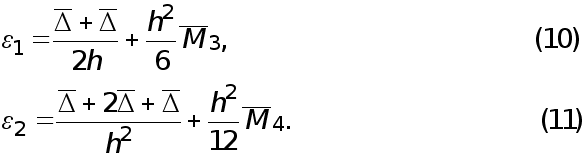Реферат: Численные методы
1.Предположим, что ![]() Тогда существует такая точка
Тогда существует такая точка ![]() , что
, что
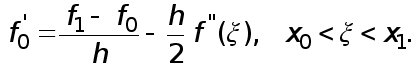 (4)
(4)
-
Если
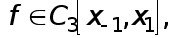 то существует такая точка
то существует такая точка 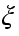 , что
, что
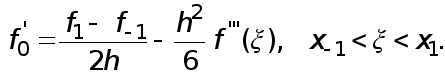 (5)
(5)
-
Когда
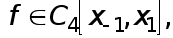 то существует
то существует 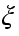 такая, что
такая, что
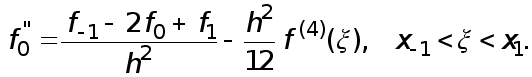 (6) Доказательство. По формуле Тейлора
(6) Доказательство. По формуле Тейлора
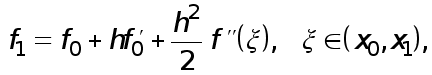
откуда следует (4).
Если ![]() то по формуле Тейлора
то по формуле Тейлора
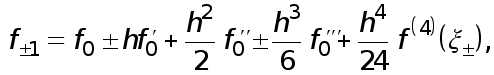 (7)
(7)
где ![]()
Подставим (7) в 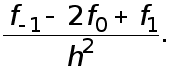 Получаем
Получаем
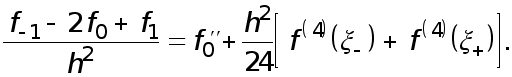
Заменяя в соответствии с леммою 1
![]()
получаем
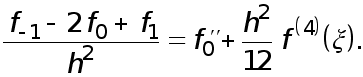
Откуда и следует (6).
Равенство (5) доказывается аналогично ( доказательство провести самостоятельно).
Формулы (4)-(6) называются формулами численного дифференцирования с остаточными членами.
Погрешности формул (1)-(3) оцениваются с помощью следующих неравенств, которые вытекают из соотношений (4)-(6):
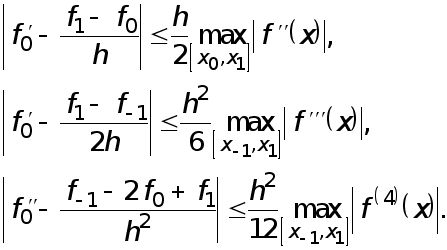
Говорят, что погрешность формулы (1) имеет первый порядок относительно ![]() (или порядка
(или порядка ![]() ), а погрешность формул (2) и (3) имеет второй порядок относительно
), а погрешность формул (2) и (3) имеет второй порядок относительно ![]() (или порядка
(или порядка ![]() ). Также говорят, что формула численного дифференцирования (1) первого порядка точности (относительно
). Также говорят, что формула численного дифференцирования (1) первого порядка точности (относительно ![]() ), а формулы (2) и (3) имеют второй порядок точности.
), а формулы (2) и (3) имеют второй порядок точности.
Указанным способом можно получать формулы численного дифференцирования для более старших производных и для большего количества узлов интерполирования.
Выбор оптимального шага. Допустим, что граница абсолютной погрешности при вычислении функции ![]() в каждой точке удовлетворяет неравенству
в каждой точке удовлетворяет неравенству
![]() (8)
(8)
Пусть в некоторой окрестности точки ![]() производные, через которые выражаются остаточные члены в формулах (5), (6), непрерывны и удовлетворяют неравенствам
производные, через которые выражаются остаточные члены в формулах (5), (6), непрерывны и удовлетворяют неравенствам
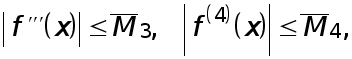 (9)
(9)
где ![]() - некоторые числа. Тогда полная погрешность формул (2), (3) (без учета погрешностей округления) в соответствии с (5), (6), (8), (9)не превосходит соответственно величин
- некоторые числа. Тогда полная погрешность формул (2), (3) (без учета погрешностей округления) в соответствии с (5), (6), (8), (9)не превосходит соответственно величин