Реферат: Численные методы

Производная равна

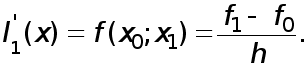
Производную функцию в точке приближенно заменяем производной интерполяционного многочлена

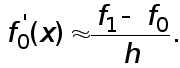(1)

Величина 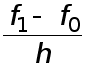называется первой разностной производной.

Пусть задана в трех точках

Интерполяционный многочлен Ньютона второй степени имеет вид

Берем производную

В точке она равна

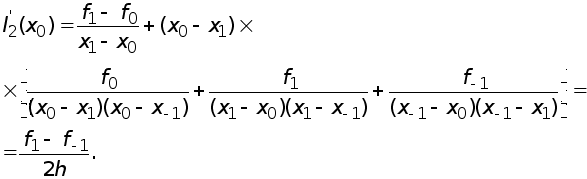
Получаем приближенную формулу

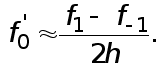(2)

Величина 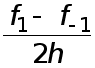называется центральной разностной производной.

Наконец, если взять вторую производную

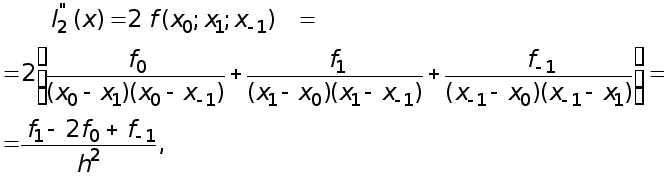получаем приближенную формулу.

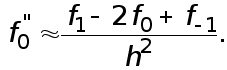(3)

Величина 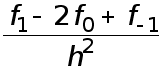называется второй разностной производной.

Формулы (1)-(3) называются формулами численного дифференцирования.

Предполагая функцию достаточное число раз непрерывно дифференцируемой, получим погрешности приближенных формул (1)-(3).

В дальнейшем нам понадобится следующая лемма.

Лемма 1. Пусть произвольные точки, Тогда существует такая точка что

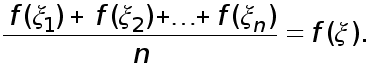
Доказательство. Очевидно неравенство

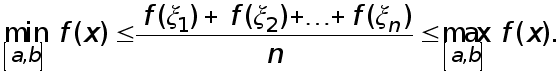
По теореме Больцано-Коши о промежуточных значениях непрерывной функции на замкнутом отрезке она принимает все значения между 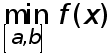и 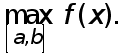Значит существует такая точка что выполняет указанное в лемме равенство.

Погрешности формул численного дифференцирования дает следующая лемма.