Дисперсия случайной величины всегда величина положительная

Размерность дисперсии равна квадрату разности случайной величины

Св-во: 1.D(c)=0

2.D(cx)=D(x)

3.D(x)=M(

Среднеквадратическое (стандартное) отклонение .

34 Мода и медиана С.В

Мода СВ наиболее вероятное значение СВ

Медиана- называет такое ее значение относит которого равновероятного получения большего или меньшего значения С.В

35 Закон распределения Дискретных С.В

Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины.

Закон распределения может быть задан аналитически, в виде таблицы или графически.

Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения .

Графическое представление этой таблицы называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.

Распределение дискретных случайных величин для некуоторых ряд распределения задается формулой бернули

36 Закон распределения непрерывных С.В

С В имеет равномерное распределение если на отрезке АВ плдотность распределения= постояннаа вне этого отрезка =0

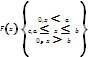
37 Нормальный Закон распределения. Правило трех сигм

Нормальный закон распределения также называется законом Гаусса .

Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.

Правило трёх сигм

При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм .

вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.

Это правило называется правилом трех сигм .

На практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.

38 Предмет мат.статистики. Основные понятия. Выборочный метод

Иследуемые признаки все объекты обладающие этим признаком образуют генеральную совокупность