Реферат: Числовой ряд

Для х<0 пользуются той же таблицей и свойством нечетности функции Лапласа, то есть Ф(-х)=-Ф(х)

Следствие: Если имеет место повторения испытания исполнения то число К в наступлении события А отличается от произведения np неболее чем на величину E по абсолютной величине. Вычисляется по формуле 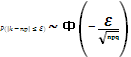частотность(m/n) событие А заключена (£<β)

Вероятность отклонения относительной частоты от постоянной вероятности вычисляется по формуле

27. наивероятнейшее число появления события

Np-q≤k0≤np+p (n - число испытаний; p - вероятность появления события при одном испытании)

1.Границы дробные k0 ед. целое число из полученного промежутка

2. Если границы целые то принимает два возможных значения имеющих одинаковую вероятность

28. Простейший поток событий

Поток событий- последовательность событий которые наступают в случайные моменты времени. Св-ва 1. Св-во стационарности-вероятность к появлению К собыбий в любой промежуток времени.

2. Св-во отсутствий последствий-взаимная независимость того или инного числа событий в непеременающие моменты времени

3 Св-во Ординарности-когда бесконечно малый промежуток времени появляется не более одного события

Поток событий который обладает св-ми стациорнарности отсутствия последственности всеми тремя назыв простейшими или пуасоновскими.

Среднее число событий которое появляется в ед времени назыв интенсивности потока.

29 Случайная величина. закон распределения вероятностей

С.В в результате принимает то или инное значение но заранее до пыта не известна

Закон распределения С.В. называют соответствие между возможными знгачениями случайной величины к соответствующими вероятности этих возможных значений

Способы задания : 1. Табличный 2. Графический 3. Аналитический

Дискретными называются случайные величины принимающие отдельные изолированные друг от друга значения, которые можно переоценить.

Ряд и многоугольник распределения.

Простейшей формой закона распределения дискретной величины является ряд распределения.

Графической интерпретацией ряда распределения является многоугольник распределения.

Непрерывными величины возможные значение которых непрерывно заполняют некоторый диапазон.

30 Функция распределения С.В и ее св-ва

Для непрерывных случайных величин применяют такую форму закона распределения, как функция распределения.

Функция распределения случайной величины Х, называется функцией аргумента х, что случайная величина Х принимает любое значение меньшее х (Х<х)

F(х)=Р(Х<х)

F(х) - иногда называют интегральной функцией распределения или интегральным законом распределения.

Св-ва:

1. F (x )определена на всей числовой прямой R ;