Реферат: Cинтез систем

Приведем полученное характеристическое уравнение к типовому виду:

где

К_ОБЩ = 500 1/с – общий коэффициент передачи усилителя;

 = 0,009 с – время чистого запаздывания;

Т₁ = 0,195 с

Т₂ = 0,005 с - постоянные времени

Т_Т = 0,05 с

тогда

а₀ = T₁T₂T_T = 4.88*10^-5 c³

a₁ = T₁T_T + T₂T_T + T₁T₂ = 0.011 c²

a₂ = T₁ + T₂ + T_T = 0.25 c

a₃ = 1 – K_ОБЩ* = - 3.5

a₄ = K_ОБЩ = 500 c^-1

Необходимое условие устойчивости: a_i > 0, для любого i = 0 .. n – не выполняется.

Проверим по критерию Гурвица:

=

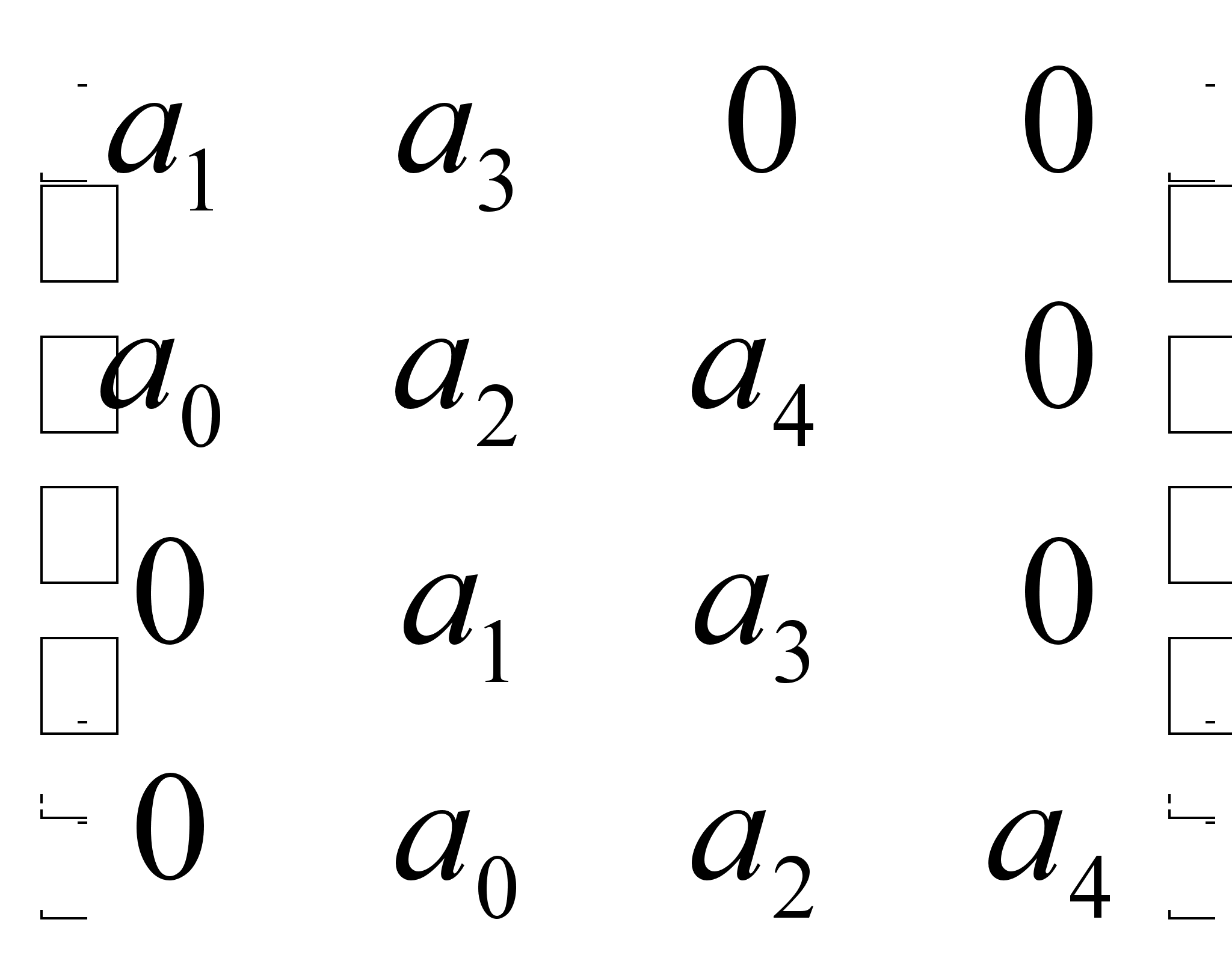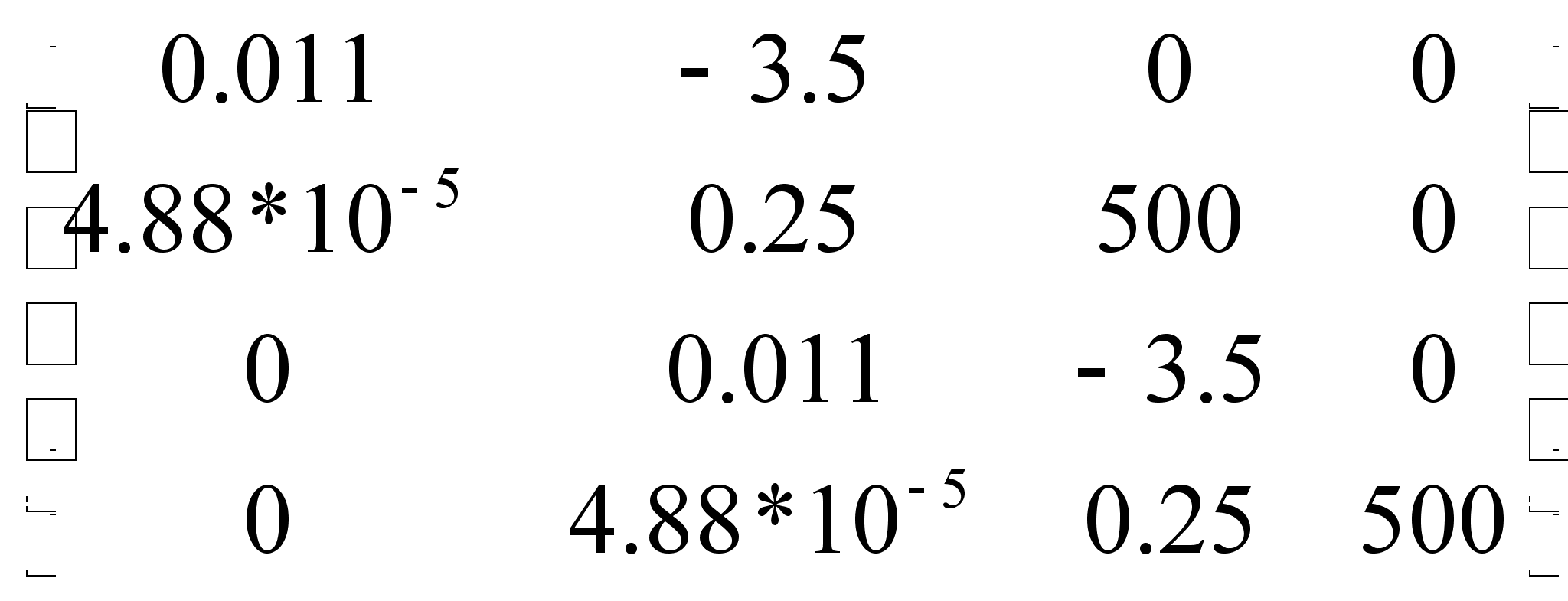
Найдем все определители матрицы:

₁ = а₁ = 0,011

₂ = а₁ а₂ – а₀ а₃= 0,00275

₃ = а₁ а₂ а₃ – а₀ а₃² – а₁² а₄ = - 0.071

₄ = а₁₃ = - 0,00078

Определители ₃ и ₄ меньше нуля и не удовлетворяют критерию Гурвица. Значит система неустойчива.

2. Исследование системы по критерию Михайлова.

Для того чтобы линейная система четвертого порядка была устойчива необходимо и достаточно чтобы вектор описывающий кривую Михайлова при изменении частоты от 0 до бесконечности поворачивался на угол 360’

Для построения кривой Михайлова используем характеристический полином полученный в предыдущем пункте.

В характеристическом полиноме выполним подстановку р = j и получим характеристический комплекс: