Реферат: Дифференциальные уравнения и описание непрерывных систем

Определитель матрицы Х1(t) представляет собой определитель Вронского. Он отличен от нуля для всех tÎ[a, b]. Следовательно, существует обратная матрица X-11(t) при каждом tÎ[а, b]. Составим матрицу

X(t, t0) = X1(t)X1-1(t0)

Столбцы этой матрицы также образуют фундаментальную систему решений системы уравнений (3). Отметим, что X(t, t0)= Назовем матрицу X(t, t0) фундаментальной матрицей системы (3). Эта матрица удовлетворяет матричному уравнению

Решение x(t) системы уравнений (3), удовлетворяющее начальным условиям x(t0)=x0, можно записать в виде

Тогда можно показать, что следующая формула, называемая формулой Коши, позволяет найти решение x(t) неоднородной системы (2), удовлетворяющее начальным условиям x(t0)=x0, если известна фундаментальная матрица X(t, t0) однородной системы (3):

Следует отметить, что если матрица А постоянная, т. е. рас­сматриваемая система дифференциальных уравнений является системой линейных уравнений с постоянными коэффициентами

то решение этой системы x(t), удовлетворяющее начальным условиям x(t0)=x0, запишется в виде

где X (f) — матрица, столбцы которой состоят из фундаменталь­ной системы решений однородной системы уравнений xt'=Ах, причем X (t0) = E.

2.7.6. Линейное уравнение n -го порядка

Линейное уравнение n-го порядка имеет вид

где a0(t), …, an(t) — непрерывные функции для tÎ(a, b), при­чем а0(t)¹0. Соответствующее этому уравнению однородное урав­нение имеет вид

Эти уравнения путем введения вспомогательных функций

можно свести соответственно к системам уравнений

или в векторной форме,

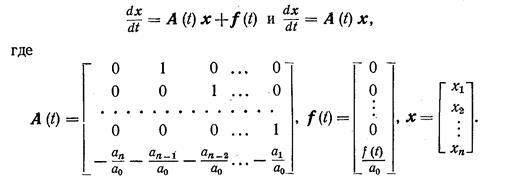
Пусть начальные условия этой системы имеют вид

Эта система имеет единственное решение

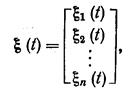
Для нахождения частного решения ф(t) данного уравнения можно использовать метод вариации произвольных постоянных. При этом система алгебраических уравнений для нахождения сi'(t) имеет следующий вид: