Реферат: Дифференциальные уравнения и описание непрерывных систем
2) yч=Q(x)eax, если a – не корень характеристического уравнения,
где Q(x) – многочлен той же степени, что и P(x), но с неопределенными коэффициентами.
2. f(x)=(Pn(x)cos(bx)+Lm(x)sin(bx))eax, где Pn (x) и Lm(x) – некоторые многочлены. Тогда частное решение ищется в виде:
1) yч=(Mn (x)cos(bx)+Nn(x)sin(bx))eax, если (a±bi) – не корень характеристического уравнения;
2) yч=xm(Mn(x)cos(bx)+Nn(x)sin(bx))eax, если (a±bi) – m-кратный корень характеристического уравнения,
где Mn(x) и Nn(x) – многочлены, степень которых равна наивысшей степени многочленов Pn(x) и Lm(x).
После выбора вида частного решения подставляем его в исходное дифференциальное уравнение. При этом неизвестные коэффициенты полиномов находим по методу неопределенных коэффициентов, который заключается в том, что неизвестные коэффициенты ищутся из условия равенства коэффициентов при одинаковых слагаемых, например, при x, при x2, при x3cos(bx) и т. д.
3. Дифференциальные уравнения при описании непрерывных систем
3.1. Составление и линеаризация дифференциальных уравнений элементов системы
В установившемся состоянии зависимость выходной величины элемента системы от входной задается статической характеристикой элемента. Как правило, статические характеристики элементов нелинейны. Статические характеристики могут быть получены из дифференциальных уравнений элементов системы.
Пусть дифференциальное уравнение, описывающее поведение элемента , имеет вид
![]() (1)
(1)
Тогда статическая характеристика этого элемента задается уравнением в неявной форме
![]() (2)
(2)
то есть для ее получения в уравнении (1) следует положить x=const и g=const.
Если динамика элемента описывается линейным дифференциальным уравнением, то этот элемент называется линейным, если дифференциальное уравнение нелинейно, то элемент называется нелинейным. Из-за нелинейности статических характеристик уравнения элементов системы в большинстве случаев являются нелинейными.
Для упрощения анализа, когда это возможно, приближенно заменяют нелинейные дифференциальные уравнения такими линейными уравнениями, решения которых с достаточной степенью точности совпадают с решениями нелинейных уравнений. Этот процесс замены нелинейного дифференциального уравнения линейным называется линеаризацией. Обычно линеаризация нелинейного уравнения производится относительно некоторого установившегося состояния элемента системы.
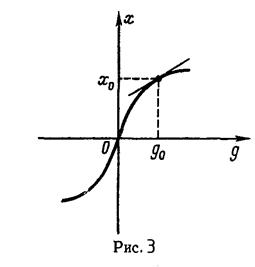
Если дифференциальное уравнение элемента нелинейно из-за нелинейности его статической характеристики, то линеаризация уравнения сводится к замене нелинейной характеристики элемента x=ф(g) некоторой линейной функцией x=ag+b. Аналитически эта замена производится с помощью разложения в ряд Тейлора функции x=y(g) в окрестности точки, соответствующей установившемуся состоянию и отбрасывания всех членов, содержащих отклонение Dg входной величины элемента в степени выше первой. Геометрически это означает замену кривой x=ф(g) касательной, проведенной к кривой в точке (х0, g0), соответствующей установившемуся состоянию работы элемента (рис. 3).
В других случаях линеаризация производится путем проведения секущей, мало отклоняющейся от функции x=ф(g) в требуемом диапазоне изменения входной величины элемента.
Назовем нелинейные статические характеристики, линеаризуемые в требуемом диапазоне изменения входной величины указанным выше способом, несущественно нелинейными характеристиками. Наряду с линеаризуемыми характеристиками имеются такие характеристики, которые не поддаются такой линеаризации. К ним относятся, например, характеристики, не разлагаемые в ряд Тейлора в окрестности точки установившегося состояния. Такие характеристики будем называть существенно нелинейными.
Рассмотрим подробнее процесс линеаризации нелинейного уравнения элемента с помощью ряда Тейлора. Пусть поведение элемента описывается нелинейным дифференциальным уравнением (1). Тогда установившееся состояние элемента характеризуется уравнением (2). Пусть g 0 и х0 — значения установившегося состояния. Тогда координаты gи х можно записать в виде х=х0+Dx, g=g0+Dg, где Dg и Dx — отклонения координат g и x от установившегося состояния. Уравнение (1) в отклонениях имеет вид
![]()
Разложим левую часть этого уравнения в ряд Тейлора относительно точки (0, 0, х0, g0):
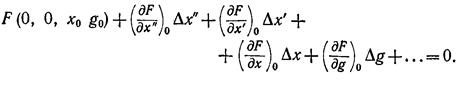
В левой части этого равенства не выписаны члены, содержащие отклонения Dg и Dx и их производные в степени выше первой. Частные производные в левой части этого уравнения представляют собой некоторые числа, величины которых зависят от вида функции F(x", x', x, g) и значений координат g0 и х0.
Считая отклонения Dg, Dх от установившегося состояния, а также их производные по времени малыми и полагая, что функция F(x", x', x, g) достаточно гладкая по всем аргументам в окрестности точки, соответствующей установившемуся состоянию, отбросим в этом уравнении все члены, которые содержат отклонения Dg и Dх, а также их производные в степени выше первой. Полученное уравнение
![]()
является линейным дифференциальным уравнением с постоянными коэффициентами
![]()
Очевидно, что необходимым условием линеаризации является возможность разложения в ряд Тейлора функции F(x", x', x, g) в окрестности точки, соответствующей установившемуся состоянию. Линеаризованное уравнение приближенно заменяет нелинейное уравнение (1) лишь в некоторой малой окрестности точки (0, 0, х0, g0). Величина этой окрестности зависит от гладкости функции F(x", x', x, g) в этой точке, т. е. от величин производных порядка выше первого этой функции в точке (0, 0, х0, g0). Как правило, с помощью линеаризованного уравнения можно исследовать поведение элемента системы лишь при малых отклонениях входной и выходной координаты от установившегося состояния. Очевидно, что необходимым условием линеаризации является возможность разложения в ряд Тейлора функции F(x", x', x, g) в окрестности точки, соответствующей установившемуся состоянию. Линеаризованное уравнение приближенно заменяет нелинейное уравнение (1) лишь в некоторой малой окрестности точки (0, 0, х0, g0). Величина этой окрестности зависит от гладкости функции F(x", x', x, g) в этой точке, т. е. от величин производных порядка выше первого этой функции в точке (0, 0, х0, g0). Как правило, с помощью линеаризованного уравнения можно исследовать поведение элемента системы лишь при малых отклонениях входной и выходной координаты от установившегося состояния.
3.2. Понятие пространства состояний