Реферат: Дифференциальные уравнения и описание непрерывных систем
Определитель этой системы есть определитель Вронского для линейно независимой системы решений x1 ,…, xn, поэтому W(t)¹0, и данная система имеет единственное решение. Интегрируя полученные значения для c'i(t), найдем ci(t) и тогда искомое решение
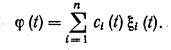
Решение x(t) исходного уравнения, удовлетворяющее заданным условиям, найдется по формуле Коши
![]()
где
![]()
где ci (t) определяются из системы уравнений
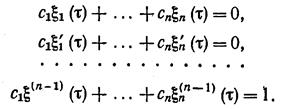
Определитель этой системы представляет собой определитель Вронского фундаментальной системы решений x1, …, xn и поэтому не равен нулю. Эта система имеет единственное решение c1(t), …, cn(t ). Следовательно, решение x1(t, t) определяется единственным образом.
2.7.7. Линейное однородное дифференциальное уравнение с постоянными коэффициентами
Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами имеет вид
![]() (5)
(5)
Его решение будем искать в виде y=ekx. Тогда y’=kekx, y’’=k2ekx, …, y(n)=knekx. Подставим это в исходное дифференциальн ое уравнение и получим так называемое характеристическо е уравнени е для дифференциального уравнения (5):
knekx +…+a2k2ekx+a1kekx+a0ekx=0
или, разделив это уравнение на ekx, так как он ни при каких x не равен нулю, получаем:
kn+…+a2k2+a1k+a0=0
Решив это уравнение относительно k, мы получим n корней, которые могут быть как действительными, так и мнимыми. В зависимости от вида корней характеристического уравнения мы будем иметь различные виды решения дифференциального уравнения:
1. Некоторые ki, …, kj из всего множества корней характеристического уравнения – действительные и различные числа. Тогда каждому km из этого множества будет соответствовать решение в виде: ym=cmekmx .
2. Некоторые ki,…, k2j – комплексные и различные. Тогда каждой паре km;m+1=am±bmi будет соответствовать решение ym=cmeamxcos(bmx); ym+1=eamxsin(bmx).
3. Среди решений характеристического уравнения есть корень ki кратности m. Ему будут соответствовать решения: yi =ciekix, yi+1=xci+1ekix, …, yi+m=xm-1ci+mekix.
4. Среди решений характеристического уравнения есть 2 комплексных корня ki;i+1=ai±bii кратности m. Им будут соответствовать решения yi =cieaixcos(bix); yi+1=ci+1eaixsin(bix); yi+2=xci+2eaixcos(bix) ; yi+3=xci+3eaixsin(bix) ; … ; yi+m=x2m-1cieaixcos(bix); yi+m=x2m-1 ´
´ci+1eaixsin(bix).
Однако, как было сказано выше, совокупность всех решений {y(x)} образует линейное пространство размерности n, так как решения этой системы являются линейно-независимыми и образуют базис. Это значит, что линейная комбинация решений линейного дифференциального уравнения также будет являться решением. Следовательно, общее решение данного линейного однородного дифференциального уравнения n-го порядка (5) с постоянными коэффициентами можно представить как линейную комбинацию решений, соответствующих каждому корню (или паре корней) характеристического уравнения.
2.7.8. Линейное неоднородное дифференциальное уравнение
Линейное неоднородное дифференциальное уравнение имеет вид
y(n)+Pn-1(x)y(n-1)+…+P2y’+P1y+P0=f(x), (6)
где P0(x), P1(x),…, Pn-1(x), f(x) – некоторые непрерывные функции, непрерывные по x и удовлетворяющие условию Липшица по x. Соответствующее ему однородное дифференциальное уравнение имеет вид
y(n)+Pn-1(x)y(n-1)+…+P2y’+P1y+P0=0, (7).
Если дифференциальное уравнение (6) имеет частное решение yв(x) и общее решение yс=c1y1+c2y2+…+cnyn, то общее решение дифференциальн ого уравнения (6) равно сумме частного решения yв и общего решения линейного однородного дифференциального уравнения (7) yc: y=yc+yв.
Методика нахождения общего решения линейного однородного уравнени я была изложена выше. Здесь мы рассмотрим нахождение частного решения линейного неоднородного уравнения.
Частное решение будет зависеть от вида правой части f(x). В общем случае трудно найти частное решение для любой функции f(x). Однако на практике применяются следующие виды функции f(x):
1. f(x)=P(x)eax, где P(x) – некоторый многочлен. Тогда частное решение ищется в виде: