Реферат: Элементы теории представлений

(II)

Подставляем это выражение в левую часть равенства 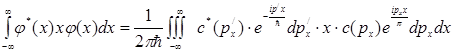(I):

(III)

Множитель в подынтегральном выражении правой части равенства найдем из соотношения:

.

Получаем:

.

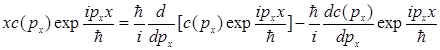Пользуясь этим соотношением, преобразуем правую часть равенства (III):

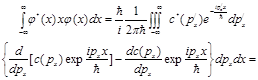
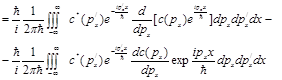(IV)

При интегрировании по получаем

,

так как и . (Состояние с бесконечно большим импульсом невозможно.) Учитывая этот результат, перепишем равенство (I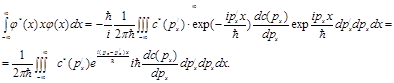V):

(V)

Так как

=

правую часть соотношения (V) можно переписать в виде

Используя свойство -функции (2.6.3) находим интеграл по :

Учитывая сделанные преобразования, переписываем равенство (V):

Сравнивая это выражении с соотношением (I) получаем

Способ 2. В матричной форме оператор координаты в импульсном представлении является бесконечной непрерывной матрицей с матричными элементами:

Здесь - собственная функция оператора импульса в координатном представлении

Подставляя значение функции в формулу для матричного элемента, получаем