Реферат: Элементы теории представлений

Соотношение

показывает как оператор в матричной форме переводит одну функцию в импульсном представлении в другую также в импульсном представлении (См(3.3.6)). Подставляем в правую часть этого соотношения значение матричного элемента и интегрируем по частям:

Первое слагаемое в правой части равно нулю, поскольку импульс не может быть бесконечно большим. Второе слагаемое преобразовываем, используя свойство -функции (2.6.3):

Поэтому

Следовательно, координате в импульсном представлении соответствует дифференциальный оператор

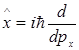
4. Задания, для контрольной проверки знаний

I. Проверить, коммутируют ли приведенные ниже операторы?

1. и

2. и

3. и , где

4. и

5. и

II . Найти операторы, сопряженные с приведенными ниже. Определить какие операторы являются эрмитовыми.

1.

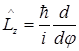
2.

3.

4.

5.

III . Доказать:

1. если операторы и эрмитовы и коммутируют, то оператор также эрмитов;

2. если операторы и эрмитовы и некоммутирующие, то оператор эрмитов;

3. если операторы и эрмитовы и некоммутирующие, то оператор эрмитов;

4. если операторы и эрмитовы и некоммутирующие, то оператор не эрмитов;

5. если оператор линейный, то оператор эрмитов;