Реферат: Компонентный и факторный анализ

- для факторных признаков найти оценку матрицы парных коэффициентов корреляции, найти собственные числа и собственные вектора;

- на основании матрицы собственных чисел определить вклад главных компонент в суммарную дисперсию признаков, отобрать и указать m (m<n) первых главных компонент, обеспечивающих уровень информативности 0.85;

- построить матрицу факторных нагрузок A и дать экономическую интерпретацию;

- по матрице наблюденных значений главных компонент F провести классификацию объектов по первым двум главным компонентам, дать интерпретацию;

- используя вектор значений результативного признака Y и матрицу F построить уравнение регрессии.

Метод общих факторов:

- оценить матрицу парных коэффициентов ;

- преобразовать матрицу в редуцированную матрицу _h ;

- получить первые три общих фактора и дать экономическую интерпретацию по матрице факторных нагрузок;

- на основе матрицы F провести графически классификацию объектов по первым двум общим факторам;

- построить функцию регрессии на выделенные общие факторы.

Введение

Наличие множества исходных признаков, характеризующих процесс функционирования объектов, заставляет отбирать из них наиболее существенные и изучать меньший набор показателей. Чаще исходные признаки подвергаются некоторому преобразованию, которое обеспечивает минимальную потерю информации. Такое решение может быть обеспечено методами снижения размерности, куда относят факторный и компонентный анализ. Эти методы позволяют учитывать эффект существенной многомерности данных, дают возможность лаконичного или более простого объяснения многомерных структур. Они вскрывают объективно существующие, непосредственно не наблюдаемые закономерности при помощи полученных факторов или главных компонент. Они дают возможность достаточно просто и точно описать наблюдаемые исходные данные, структуру и характер взаимосвязей между ними. Сжатие информации получается за счет того, что число факторов или главных компонент – новых единиц измерения – используется значительно меньше, чем было исходных признаков.

1. Исследование на мультиколлинеарность объясняющие пере­менные.

Приведем результаты по исследованию на мультиколлинеарность:

1) Коэффициенты корреляционной матрицы для объясняющих переменных не превышают 0,75, то есть тесная линейная связь между компонентами не подозревается.

2) Найдем определитель матрицы X^T X, det(X^T X)= 1.425E+6 - мал. Необходимое условие мультиколлинеарности (плохой обусловленности системы).

3) В численных методах обусловленность системы характеризуется числом обусловленности М

, где - собственные числа матрицы системы линейных уравнений.

Если число обусловленности велико, то система плохо обусловлена (порядка выше 10).

Собственные числа матрицы =2.292, =1.042, =0.952, =0.659, =0.055.

- велико система плохо обусловлена.

4) Анализ корреляционной матрицы позволяет лишь в первом приближении (и относительно поверхностно) судить об отсутствии мультиколлинеарности в наших исходных данных. Более внимательное изучение этого вопроса достигается с помощью расчёта значений коэффициентов детерминации каждой из объясняющих переменных на все остальные.

Проверим с уровнем значимость множественных коэффициентов корреляции.

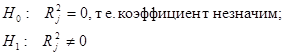
Строим статистику:

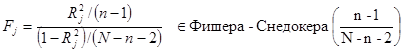
Если