Реферат: Компонентный и факторный анализ

Сумма матриц даёт:

Представим матрицы индивидуальных значений общих и характерных фак­торов. Иногда для удобства их представляют в одной матрице:

Модель (1) можно записать в матричной форме:

3.1 Преобразование матрицы парных коэффициентов корреляции в редуцированную матрицу.

Запишем корреляционную матрицу:

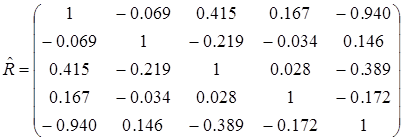
Следующим шагом будет – построение редуцированной матрицы кор­реляции с общностями на главной диагонали. Общность показывает какую часть, какую долю составляет относительно дисперсии каждого из m общих факторов в дисперсии I - го исходного признака. Существуют следующие методы нахождения общности:

a) наибольшего элемента метод по строке

Суть метода заключается в том, что в строке матрицы , соответствующей данному признаку, выбирается элемент с наибольшим абсолютным значе­нием. Это наибольшее значение коэффициента корреляции записывается на главной диагонали.

h= 0,940 h=0,219 h=0,415 h=0,172 h=0,940

b) метод среднего коэффициента корреляции

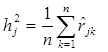
h= 0,3977 h=0,1175 h=0,2627 h=0,10025 h=0,4117

с) метод триад

В j – ом столбце или строке отыскивают два наибольших значения ко­эффициентов корреляции и , тогда

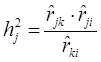
h= 0,2314 h=0.0821 h=0,1717 h=0,0306 h=0,1956

d) метод первого центроидного фактора

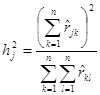
h= 0,6562 h=0,8181 h=0,9407 h=0,2054 h=0,4315

Запишем матрицу , используя метод среднего коэффициента корреляции:

h= 0,3977 h=0,1175 h=0,2627 h=0,10025 h=0,4117

Построим матрицу Rh – редуцированную корреляционная матрица.

Для получения первого вектора коэффициентов первого главного фактора необходимо найти наибольшее собственное число матрицы и по нему построить соответствующий собственный вектор, затем нормировать его и умножить все компоненты этого вектора на ( для того, чтобы длина этого вектора была ), тогда получим искомый вектор .Затем необходимо найти матрицу рассеивания , обусловленную влиянием первого общего фактора, и матрицу остатков, которая содержит в себе связи, обусловленные влиянием всех общих факторов, начиная со второго. Далее переходим по той же схеме к поиску собственных чисел матрицы . Но, оказывается, что собственные числа и собственные вектора матриц и совпадают, начиная со второго, а это означает, что достаточно найти собственные числа матрицы , ранжировать их и найти собственные вектора.

Получим следующие собственные числа:

₁ =1.658 ₂ =0.21 ₃ =0.069 ₄ =-0.105 =-0.542