Реферат: Лекции по Математическому анализу

А может быть конечным или бесконечным

Если последовательность имеет конечный предел, то она называется сходящейся, а если нет – расходящейся.

2. Общие свойства сходящихся последовательностей аналогичны свойствам ф-ий, имеющих конечный предел.

3. Арифметические свойства сходящихся последовательностей аналогичны свойствам ф-ий, имеют конечный предел

4. Переход к пределам в неравенствах, для сходящихся последовательностей аналогичен ф-ям, имеющим конечный предел.

5. Определение бесконечно малых и бесконечно больших последовательностей и их свойства аналогичны соответствующим определениям и свойствам ф-ии непрерывного аргумента.

Критерии существования предела последовательности

1. Критерии Коши (произведения последовательностей)

Для существования предела последовательностей необходимо и достаточно, чтобы для любой..............

Последовательность, для которой выполняется признак Коши – фундаменталная

2. Критерий Вейерштрасса (монотонность последовательности)

а) неубывающие последовательности, ограниченные сверху, имеют предел.

б) не возрастающие последовательности, ограниченные снизу, имеют предел.

Доказательство(а):

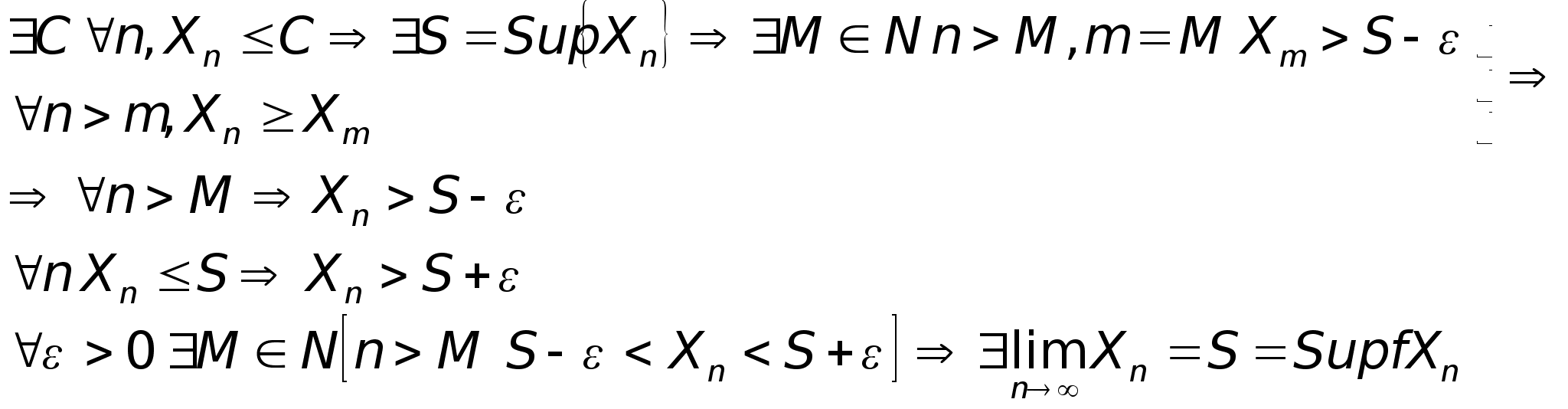
Переход к пределу в неравенстве

Теорема: Пусть f(х) и (х) имеют конечные пределы в т. y=a, тогда справедливо:

1. 

2. 

3. 

4. 

Доказательство:

1. Пусть 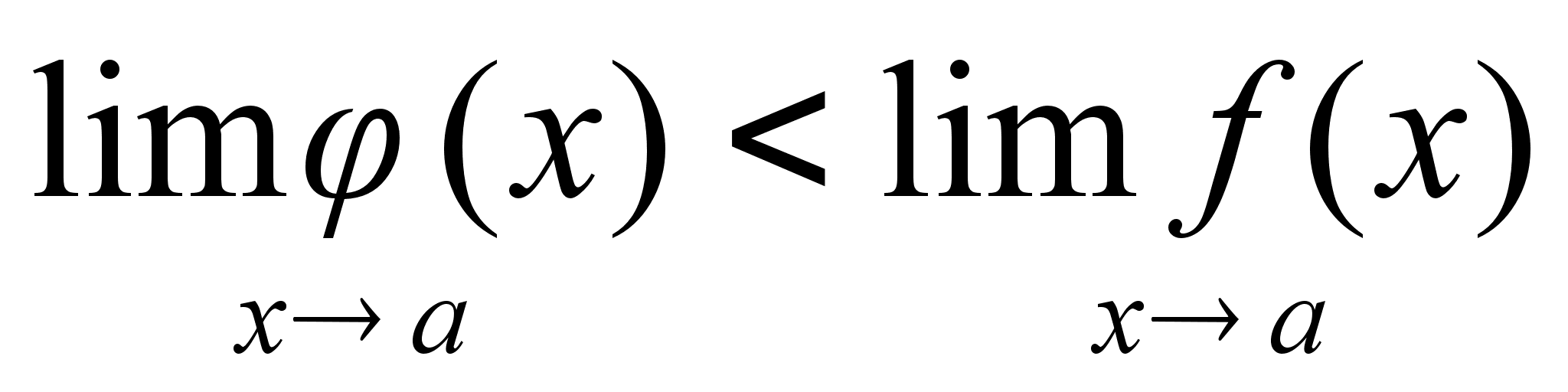, тогда по общему свойству №6

,

а это противоречит 1

Замечание:

1. Из утверждения №3 следует, что предел неотрицательной ф-ии является неотрицательным.

2. При пределов к противоположным можно обе части умножать на (-1).