Реферат: Лекции по Математическому анализу
Частные случаи (геометрическая иллюстрация)
Конечный предел в конечной т.
а – вещественное число
Общие свойства конечного предела
-
Если
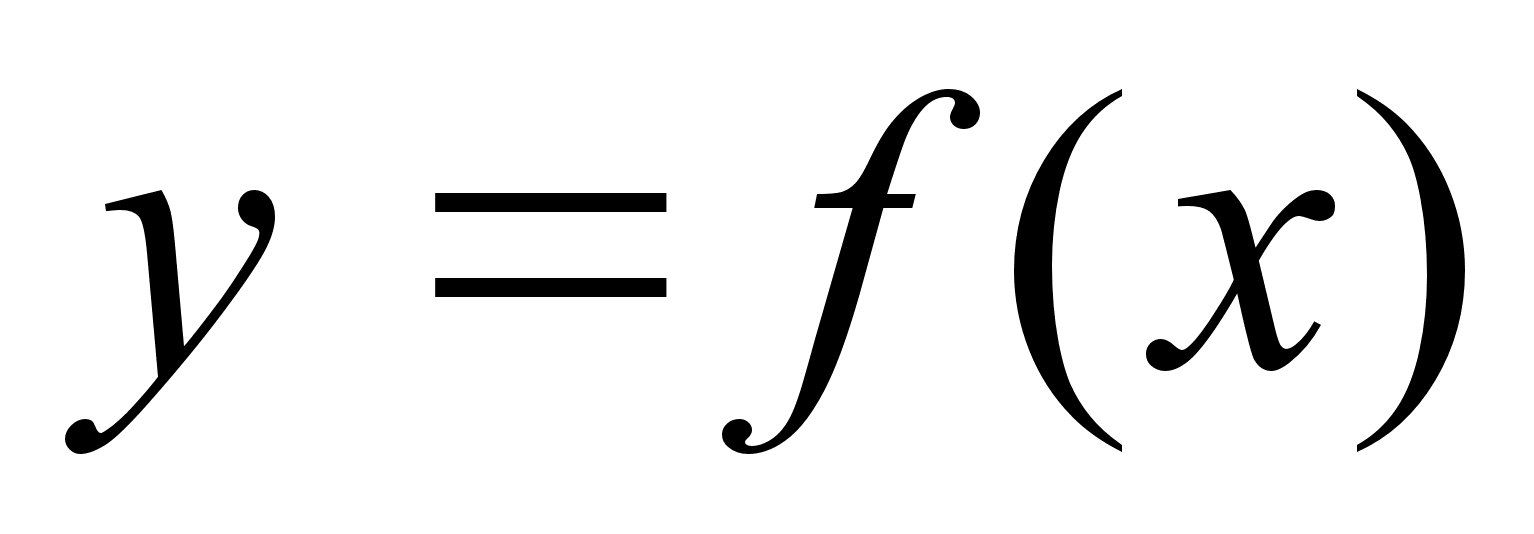- const, то ее предел сущ. и равен этой же const.
, то
-
Если конечный предел сущ., то он единственный
-
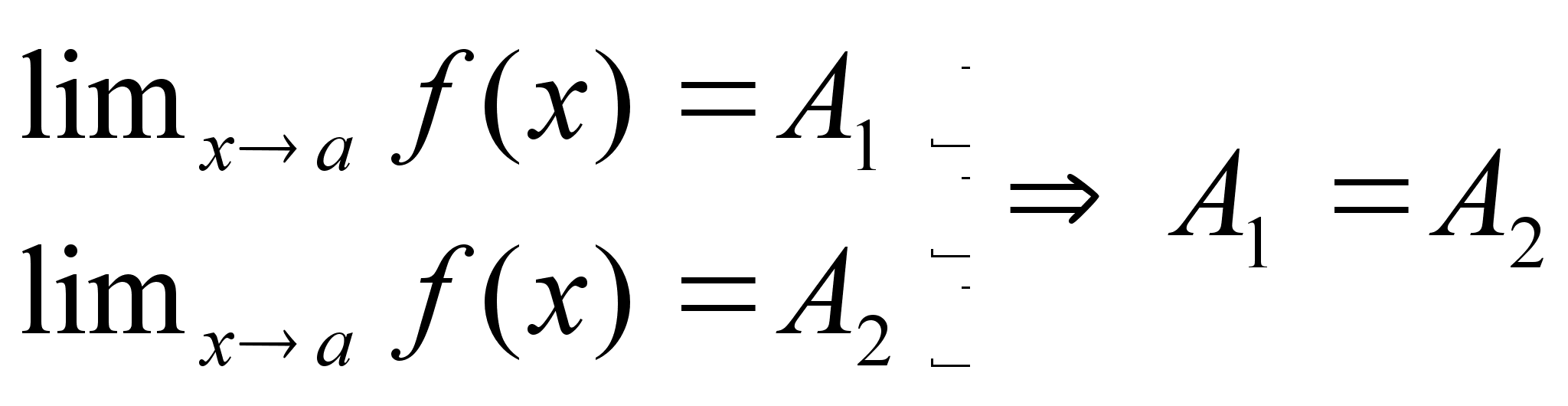
Для f(x), имеет конечный предел в т. а, сущ. такая прколотая окрестность этой т., в которой ф-ия ограничена.
-
Если ф-ия имеет в т. а, конечный предел, неравный нулю то найдется такая
в т. а, в которой 
- ограниченная. 
-
Если f(x), имеет в т. а отрицательный конечный предел, то найдется такое значение этой точки, в котором ф-ия отрицателная.
Бесконечно малые ф-ии и их свойства:
Опр:- бесконечно малая при 
, если 
Свойства:
Пусть и 
являются бесконечно малыми при , а 
- ограничена, то бесконечно малыми является алгебраическая сумма ф-ий f(x) и (x), произведения их и произведения ф-ий на ограниченную.
Представвление ф-ии, имеющей конечный предел.
Теорема: Для того чтобы ф-ия имела конечный предел А в точке х=а, небходимо и достаточно, чтобы =А+(х), где (х)- бесконечно малая при .
Доказательство:
Алгебраические свойства фунцций имеющих конечный предел в точке а.
Пусть 
, тогда: