Реферат: Лекции по Математическому анализу

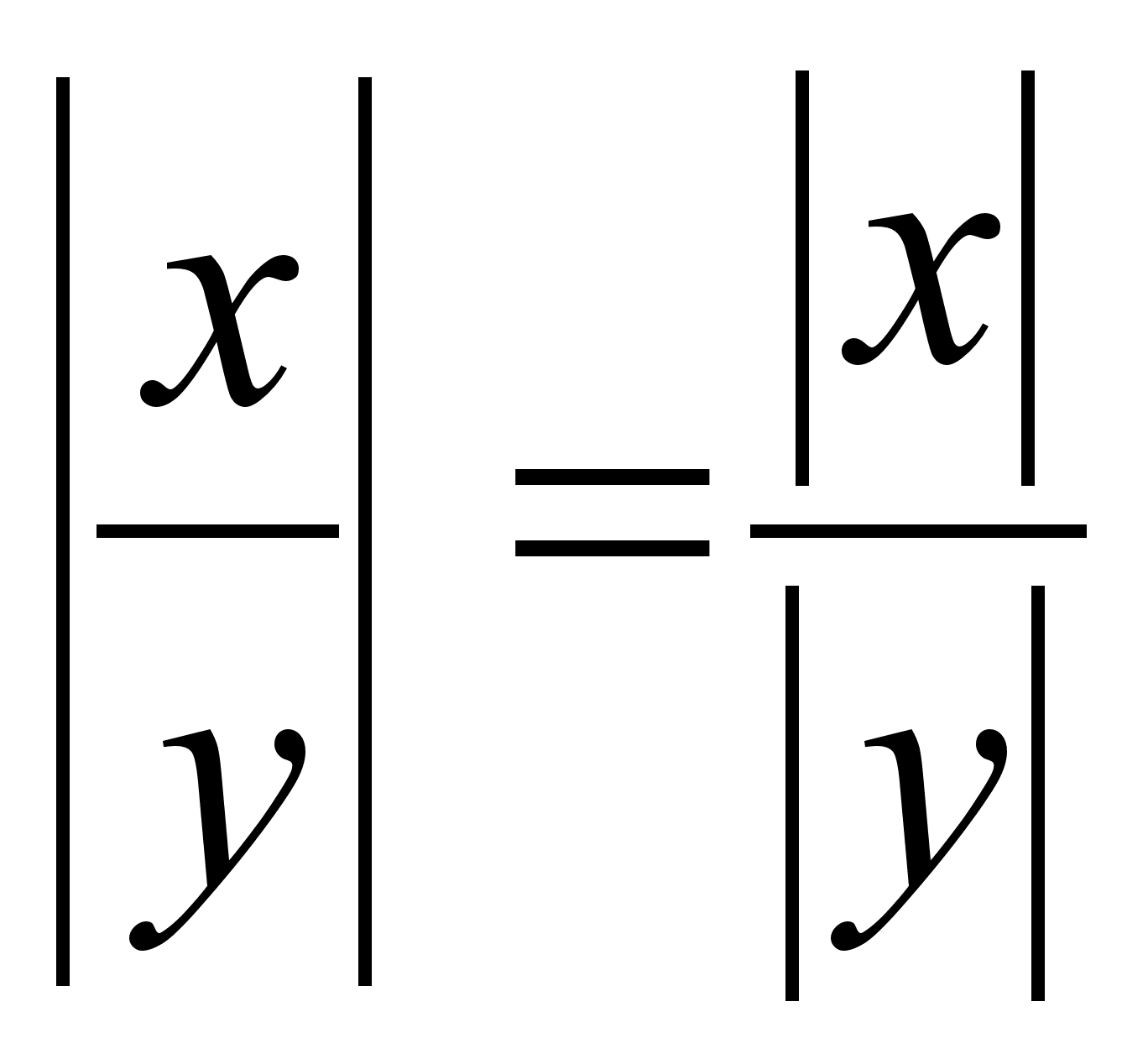
Решение простейших неравенств с модулем.

Эквивалентность неравенств:

геометрический смысл:

Понятие  окрестности в точке х₀

 окрестности в точке х₀ (U_ (x₀)) – симметричный интервал радиуса  с центром в точке х₀

Приколотой  окрестности в точке х₀ называется  окрестности этой точки без самой х₀

Открытые и замкнутые множества

Множество - называется открытым, если для любой точки этого множества найдется такая , которая целиком содержится в этом множестве.

, точки, обладающие этими свойствами, называются внутренними точками.

(a,b) – открытое множество:

Точка x X B любой окружности содержит – граничной точки множества X

Точки a и b – граничные [a;b] или (a;b).

Граничные точки могут и принадлежать, и не принадлежать множеству отрицательных. Множество своих границ не содержит.

Точка x называется предельной точкой X, если любое - окружности содержит хотя бы точек X.

(x-предельная для X) ( (x) ( x, x) (x, (x) )

точки a,b являются предельными как для отрезка, так и для интервала ( [a;b] и (a;b) )