Реферат: Лекции по математике
Определение 3. Произведением матрицы на число называется матрица того же размера, каждый элемент которой равен произведению соответствующего элемента исходной матрицы на это число..
Определение 4. Произведением двух матриц А и В , размеры которых заданы соотношением: количество столбцов первой матрицы равно количеству строк второй, называется матрица С , у которой количество строк равно количеству строк первой матрицы, а количество столбцов равно количеству столбцов второй. Каждый элемент данной матрицы равен сумме попарных произведений элементов соответствующей строки первой матрицы и элементов соответствующего столбца второй.
Приведем свойства операций над матрицами.
1. А · В ![]() В · А - произведение матриц не комму-тативно.
В · А - произведение матриц не комму-тативно.
2. А+В = В+А - сложение матриц коммутативно.
3. (А + В) +С = А + (В + С) - ассоциативность.
4. А · Е=Е · А=А.
5. ![]() .
.
6. ![]() .
.
7. ![]() .
.
1.1.3. Определители
Пусть дана квадратная матрица порядка n :
А = 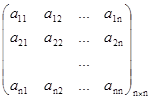 .
.
Определение 1. Определителем n -го порядка матрицы А называется число, равное алгебраической сумме n ! слагаемых, каждое из которых равно произведению n элементов матрицы А ![]() , взятых по одному из каждой строки и каждого столбца, причем каждое слагаемое берется со знаком "+" или "-".
, взятых по одному из каждой строки и каждого столбца, причем каждое слагаемое берется со знаком "+" или "-".
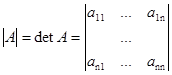 .
.
Пример 1. Определитель второго порядка. n =2, 2!=1 · 2=2 слагаемых.
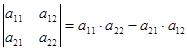 .
.
Мнемоническое правило вычисления определителя второго порядка:
![]()
слагаемое со знаком "-", слагаемое со знаком "+".
Пример 2. Определитель третьего порядка. n =3, 3!=1 · 2 · 3=6 слагаемых,
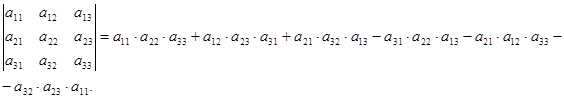
Мнемоническое правило вычисления определителя третьего порядка:
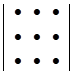
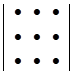
слагаемые со знаком "+", слагаемые со знаком "-".
Можно построить мнемонические правила для вычисления определителей порядка выше чем три, но они будут слишком громоздкими. Поэтому вычисление таких определителей основано на свойствах определите
1.1.4.Свойства определителей
Теорема 1. При транспонировании величина определителя не меняется.
Следствие. Строки и столбцы в определителе равноправны, т.е. свойства, справедливые для строк, будут справедливы и для столбцов.