Реферат: Лекции по математике

Следствие. Постоянный множитель строки можно выносить за знак определителя.

Теорема 3. Если в определителе поменять местами две строки, то определитель сменит знак на противоположный.

Следствие 1. Определитель, у которого две строки равны, равен нулю.

Следствие 2. Если в определителе две строки пропорциональны, то такой определитель равен нулю.

Теорема 4. Если строка определителя представлена в виде алгебраической суммы нескольких слагаемых, то определитель равен алгебраической сумме определителей, у которых в первом определителе в данной строке стоит первое слагаемое, во втором - второе слагаемое и т.д.

Следствие. Если строки определителя линейно зависимы , то такой определитель равен нулю.

Теорема 5. Если к элементам одной строки определителя прибавить соответствующие элементы другой, умноженные на одно и то же число, то определитель не изменится.

1.1.5. Миноры и алгебраические дополнения

Пусть дана прямоугольная матрица А размера .

Определение 1. Минором порядка k данной матрицы, где k min(m ;n ), называется определитель k -го порядка , полученный из матрицы А вычеркиванием (m-k ) строк и (n-k ) столбцов.

Пример А =, ,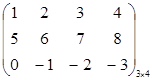

.

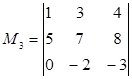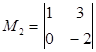Определение 2. Дополнительным минором M _ij к элементу a _ij квадратной матрицы называется определитель (n -1) порядка, полученный из матрицы А вычеркиванием этого элемента вместе со строкой и столбцом, в которых он расположен.

Пример. .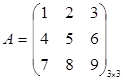

Найдем дополнительный минор к элементу a ₃₁ . .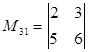

Определение 3. Алгебраическим дополнением A _ij к элементу a _ij квадратной матрицы называется число A _ij = .

Пример. Найдем алгебраическое дополнение к элементу a ₃₃ .

.

Теорема 1. Определитель равен сумме попарных произведений элементов любой строки на их алгебраические дополнения.

- разложение определителя по i -й строке.

Вычисление определителей порядка n >3 сводится к вычислению определителей второго и третьего порядка с помощью теоремы 1 и свойства 5 определителя.

1.1.6. Обратная матрица

Определение 1. Квадратная матрица называется вырожденной, если ее определитель равен нулю, и невырожденной - в противном случае.

Определение 2. Матрица А ^-1 называется обратной к квадратной матрице А n -го порядка, если А ·А ^-1 = А ^-1 ·А =Е .

Теорема 1. Для любой невырожденной квадратной матрицы существует единственная обратная матрица.

Дана матрица А = , .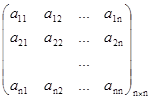

Построим обратную матрицу. Для этого совершим ряд действий:

1) заменим все элементы матрицы их алгебраическими дополнениями :

А*= 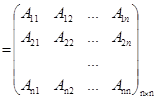- матрица, присоединенная к матрице А ;

2) транспонируем полученную матрицу :

(А *)^Т =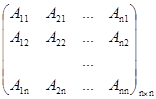;