Реферат: Лекции по математике

Раздел 1. Элементы линейной алгебры.

1.1 Матрицы, определители.

Вопросы:

1.1.1. Определение матриц, виды матриц;

1.1.2. Операции над матрицами;

1.1.3. Определители;

1.1.4. Свойства определителей;

1.1.5. Миноры и алгебраические дополнения;

1.1.6. Обратная матрица. Нахождение обратной матрицы;

1.1.7. Элементарные преобразования матриц. Ранг матрицы.

1.1.1. Матрицы

Определение 1. Прямоугольная таблица чисел вида

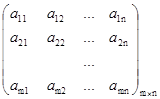
называется прямоугольной матрицей размера , где m - количество строк, а n - количество столбцов.

Определение 2. Числа, которые образуют матрицу, - a _ij , где , , называются элементами матрицы.

Определение 3. Числа i и j называются индексами элемента a _ij , i показывает, в какой строке расположен данный элемент, а j - в каком столбце находится этот элемент.

Две матрицы считаются равными, если равны их соответствующие элементы.

Виды матриц.

Если m =n , то матрица называется квадратной матрицей порядка n .

Матрица размера называется матрицей-столбцом.

.

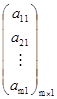Матрица размера называется матрицей-строкой.

.

Определение 1. Элементы матрицы , имеющие равные индексы , образуют главную диагональ матрицы.

Определение 2. Квадратная матрица называется диагональной, если все элементы вне ее главной диагонали равны нулю.

Определение 3. Диагональная матрица n -го порядка, у которой диагональные элементы равны единице, называется единичной матрицей n -го порядка и обозначается Е .

Определение 4. Матрица называется матрицей треугольного вида, если все элементы над (под) главной диагональю равны нулю.

Примеры. , .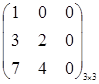

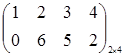1.1.2. Операции над матрицами

Определение 1. Транспонированием матрицы называется такое преобразование матрицы, при котором строки и столбцы меняются ролями при сохранении номеров. Транспонированная матрица обозначается А ^Т .

, , .

Для квадратной матрицы это преобразование эквивалентно симметричному отображению относительно главной диагонали.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--