Реферат: Матричный анализ

Составим дробно-рациональную функцию:

и разложим ее на простейшие дроби.

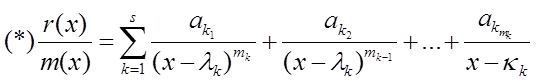
Обозначим: . Умножим (*) на и получим

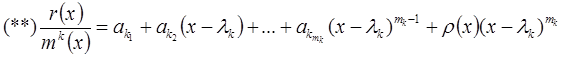
где – некоторая функция, не обращающаяся в бесконечность при .

Если в (**) положить , получим:

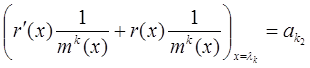
Для того, чтобы найти a_k3 надо (**) продифференцировать дважды и т.д. Таким образом, коэффициент a_ki определяется однозначно.

После нахождения всех коэффициентов вернемся к (*), умножим на m(x) и получим интерполяционный многочлен r(x), т.е.

.

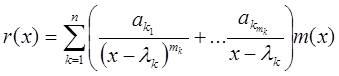Пример: Найти f(A), если , где t – некоторый параметр,

.

Найдем минимальный многочлен матрицы А:

.

Проверим, определена ли функция на спектре матрицы А

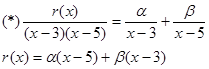
Умножим (*) на (х-3)

при х=3

Þ

Умножим (*) на (х-5)

.

Таким образом, - интерполяционный многочлен.

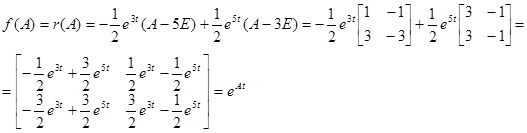
Пример 2.

Если 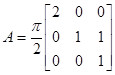, то доказать, что