Реферат: Матричный анализ

(A+E)=2Z₂₁ +Z₃₁ +Z₁₂

3. f(x)=(x+1)²

(A+E)² =4Z₂₁ +Z₃₁

4. f(x)=x-1

A-E=-2Z₁₁ +Z₁₂ -Z₃₁

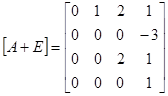
1. f(x)=1 E=Z₁₁ +Z₂₁ +Z₃₁

2. f(x)=x+1 A+E=Z₁₁ Z₂₂ +2Z₃₁

3. f(x)=(x+1)² (A+E)² =Z₁₁ +4Z₃₁

4. f(x)=x-1 (A-E)=-Z₁₁ -2Z₂₁ +Z₂₂

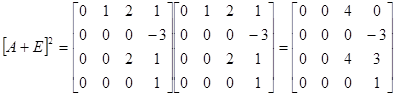
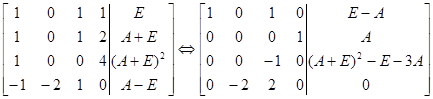
Z₃₁ =A

-Z₂₂ =(A+E)² -E-3A

Z₁₂ =Z₂₂

Z₁₁ =(E-A)-Z₂₂

6.Определенные матрицы.

Эрмитовы и квадратичные матрицы.

Пусть А – эрмитова матрица (А^* =А).

Рассмотрим функцию h(x) – действительная функция комплексного аргумента.

Рассмотрим:

DF . Функция , где А – эрмитова матрица, называется эрмитовой формой от n переменных x₁ , …, x_n , где А – матрица эрмитовой формы.

Очевидно, что если А – действительная симметрическая матрица, то в этом случае получаем квадратичную форму .

Для каждой эрмитовой (квадратичной) формы инвариантами являются: ранг (число не нулевых коэффициентов в квадратичной форме нормального вида совпадающих с рангом матрицы А), p (индекс) – число положительных коэффициентов в квадратичной форме нормального вида, оно совпадает с числом положительных собственных значений, сигнатура . Эти числа r, p, гр-r не зависят от тех преобразований, которые совершаются над данными формами.

В дальнейшем ограничимся рассмотрением только квадратичных форм. Нас интересуют 2 семейства матриц.

DF . Действительная симметрическая матрица А называется положительно определенной , если для .

DF . Действительная симметрическая матрица А называется неотрицательно определенной , если для .

Оба типа матриц относятся к классу определенных матриц. Заметим, что положительно определенная матрица невырожденная, т.е. если предположить, что она вырожденная, то , , что противоречит условию.

Теорема № 1. Действительная симметрическая матрица n-го порядка будет определенной ранга тогда и только тогда , когда она имеет r положительных собственных значений, а остальные (n-r) – собственные значения равны 0.

Теорема № 2. Действительная симметрическая матрица положительна определена тогда и только тогда, когда все ее главные миноры положительны.