Реферат: Нечеткие множества в системах управления

T(m_A , T(m_B , m_C )) = T(T(m_A , m_B ), m_C ) - ассоциативность .

Примеры t -конорм:

max(m_A , m_B )

m_A + m_B - m_A ×m_B

min(1, m_A + m_B ).

Алгебраические операции над нечеткими множествами

Алгебраическое произведение A и B обозначается A ×B и определяется так:

"x ÎE m_{A ×B} (x ) = m_A (x ) m_B (x ).

Алгебраическая сумма этих множеств обозначается и определяется так:

" x Î E = m _A (x ) + m _B (x ) -m _A (x ) m _B (x ).

Для операций {×, } выполняются свойства:

- коммутативность;

- ассоциативность;

A×Æ = Æ, AÆ = A, A×E = A, AE = E

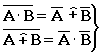- теоремы де Моргана.

Не выполняются:

- идемпотентность;

- дистрибутивность;

а также A× = Æ, A= E.

Замечание . Доказательства приводимых свойств операций над нечеткими множествами мы оставляем читателю.

Для примера докажем свойство: . Обозначим m_A (x ) через a , m_B (x ) через b . Тогда в левой части для каждого элемента х имеем: 1-ab , а в правой: (1-a )+(1-b )-(1-a )(1-b ) = 1-a +1-b - 1+a +b-ab = 1-ab . 

Докажем, что свойство дистрибутивности не выполняется, т.е. A ×(BC) ¹ (A ×B)(A ×C) . Для левой части имеем: a (b +c-bc ) = ab +ac-abc ; для правой: ab +ac -(ab )(ac ) = ab +ac +a ² bc . Это означает, что дистрибутивность не выполняется при a ¹a ² . 

Замечание. При совместном использовании операций {È, Ç,+,×} выполняются свойства:

А×(BÈC) = (A×B)È(A × C);

А× (BÇC) = (A×B)Ç(A×C);

А(BÈC) = (AB)È(AC);

А(BÇC)=(AB)Ç(AC).

Продолжим обзор основных операций над нечеткими множествами.

На основе операции алгебраического произведения (по крайней мере для целых a эта основа очевидна) определяется операция возведения в степень a нечеткого множества A , где a - положительное число. Нечеткое множество A a определяется функцией принадлежности m_A ^a = m^a _A (x) . Частным случаем возведения в степень являются:

CON(A) = A² - операция концентрирования ,