Реферат: Нечеткие множества в системах управления
A = 
aA a , где aA a - произведение числа a на множество A , и a "пробегает" область значений M функции принадлежности нечеткого множества A .
Пример: A = 0,1/x 1 + 0/x 2 + 0,7/x 3 + 1/x 4 представимо в виде:
A = 0,1(1,0,1,1) È 0,7(0,0,1,1,) È 1(0,0,0,1)=
= (0,1/x1 + 0/x2 + 0,1/x3 + 0,1/x4 )È (0/x1 + 0/x2 + 0,7/x3 + 0,7/x4 )È
È(0/x1 + 0/x2 + 0/x3 + 1/x4 ) = 0,1/x1 +0/x2 +0,7/x3 +1/x4 .
Если область значений функции принадлежности состоит из n градаций a1 £a2 £a3 £ ...£an , то A (при фиксированных значениях градаций) представимо в виде:
A = 
a i A a i ,
т.е. определяется совокупностью обычных множеств { A a1 , A a2 , ..., A ai }, где A a1 ³A a2 ³ , ..., ³A ai .
Расстояние между нечеткими множествами, индексы нечеткости
Пусть A и B - нечеткие подмножества универсального множества E . Введем понятие расстояния r(A , B ) между нечеткими множествами. При введении расстояния обычно предъявляются следующие требования:
r(A, B ) ³ 0 - неотрицательность;
r(A, B ) = r(B, A ) - симметричность;
r(A, B ) < r(A, C ) + r(C, B ).
К этим трем требованиям можно добавить четвертое: r(A, A ) = 0.
Определим следующие расстояния по формулам:
Расстояние Хемминга (или линейное расстояние ):
r(A, B ) = 
½m A (xi ) - m B (xi )½ .
Очевидно, что r(A, B )Î[0, n ].
Евклидово или квадратичное расстояние:
e(A, B ) =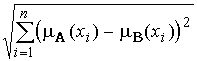 
, e(A, B )Î[0, 
].
Относительное расстояние Хемминга:
r(A, B ) = 
, r(A, B )Î[0,1].
Относительное евклидово расстояние:
e(A, B )=
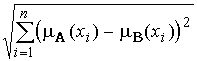, e(A, B )Î[0,1].
Расстояние Хемминга и квадратичное расстояние, в случае когда E бесконечно, определяются аналогично с условием сходимости соответствующих сумм:
если E счетное, то
r(A, B ) = 
½m A (xi ) - m B (xi )½ ,
e(A, B ) = 
;
если E = R (числовая ось), то
r(A, B ) =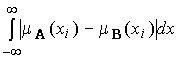 
,