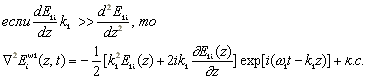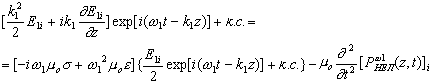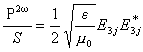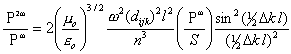Реферат: Нелинейная оптика

(8)

Дифференцируем и полагаем, что изменение комплексных амплитуд полей достаточно медленное, т.е.

(9)

Аналогичные выражения можно вывести для С² E_j ^{w 3} (z,t) и С² E_k ^{w 2} (z,t). Подставляя (9) в (6) и используя соотношение ¶/¶t=iw₁ получим волновое уравнение для E_i ^{w 1} (z,t):

(10)

Предполагаем, что при взаимодействии конечного числа полей уравнение (6) должно удовлетворяться по отдельности для компонент с различными частотами. Поставив (7а) и заметив, что w₁ ² m₀ e=k₁ ² , получим

(11)

или (считая s функцией частоты)

(11a)

и аналогично

(11b)

(11c)

Эти уравнения мы применим в дальнейшем при рассмотрении ряда конкретных случаев.

Генерация второй гармоники (ГВГ)

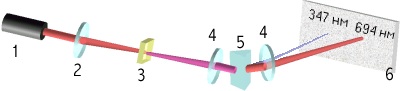
Первый эксперимент по генерации второй гармоники света был выполнен Франкеном в 1961 году. Луч рубинового лазера с l = 694,3 нм фокусировался на поверхность пластины из кристаллического кварца. Выходящее излучение анализировалось спектрометром. Было найдено, что в нем содержится компонента с удвоенной частотой (т.е. с l = 347,15 нм). Эффективность преобразования в первых экспериментах была порядка 10^-8 . Использование более эффективных материалов, увеличение мощности лазера, обеспечение условий фазового синхронизма позволили в последние годы довести коэффициент преобразования почти до единицы.

Рис.1. Схема первых экспериментов по ГВГ. 1 - рубиновый лазер, 2 - фокусирующая линза, 3 - кварцевая пластинка, 4 - коллиматорные линзы, 5 - призма, 6 - фотопластинка (экран). Цвета показаны условно.

Применим уравнения (11a-11c) для рассмотрения ГВГ. Это частный случай взаимодействия полей трех частот, когда две частоты w₁ и w₂ одинаковы, а w₃ = 2 w₁ . Следовательно, необходимо анализировать только два уравнения: первое (или второе) и последнее. В целях упрощения будем считать, что потери мощности входного луча (w₁ ) за счет преобразования во вторую гармонику малы, т.е. dE_1i /dz » 0. Следовательно, можно рассматривать только последнее уравнение (11c). Если среда прозрачна на частоте w₃ , то s₃ =0 и

(12)

где w = w₁ = ¹ /₂ w₃ , Dk = k₃ ^(j) - k₁ ⁽ⁱ⁾ - k₁ ^(k) , а k₁ ⁽ⁱ⁾ - волновое число волны с частотой w₁ , поляризованной по оси i. Если E_3j (0) = 0, т.е вторая гармоника на входе отсутствует, и кристалл имеет длину l, решением (12) будет

(13)

или

(14)

где e¦e₃ . Чтобы получить выражение для мощности второй гармоники P^{2 w} на выходе, воспользуемся соотношением

(15)

где S - площадь поперечного сечения пучка. Приняв e₁ »e₃ »e₀ n² приходим к коэффициенту преобразования

(16)

Фазовый синхронизм при генерации второй гармоники

Из (16) следует, что предпосылкой для эффективной ГВГ является выполнение условия Dk = 0, или, поскольку w₃ = 2 w, а w₁ = w₂ = w,

Dk = k 2 w - 2 k w = 0 ® k 2 w = 2 k w

(17)

Если Dk ¦ 0, то волна удвоенной частоты, генерируемая в некоторой плоскости (z₁ ), дойдя до другой плоскости (z₂ ), окажется не в фазе с волной удвоенной частоты, генерируемой в этой плоскости. Результат интерференции таких волн представлен в (16) множителем (¹ /₂ Dk l)^-2 sin² (¹ /₂ Dk l). Два соседних максимума этой интерференции удалены на расстояние, называемое "когерентной длиной":

(18)

Она является в сущности максимальной длиной кристалла, которую можно использовать для ГВГ. Показатель преломления, как правило, растет с увеличением частоты, так что

« 1 2 3 4 5 6 7 8 9 » К-во Просмотров: 899 Бесплатно скачать Реферат: Нелинейная оптика >>> Скачать <<< Меню Поиск