Реферат: Нелинейная оптика
Алифатические соединения
1974-2260
C¦C
Алифатические соединения
2150-2245
C¦N
Нитрилы
4160
H-H
H2
Характерно, что частоты мало меняются от соединения к соединению.
Если среду, способную к комбинационному рассеянию, поместить в оптический резонатор, то при наличии поля лазерной накачки усиление стоксовой компоненты способно скомпенсировать потери, и на частоте wc возникает генерация. Генерация при ВКР представляет собой практический способ преобразования излучения импульсных лазеров (например, лазера на неодимовом стекле) в когерентное излучение, сдвинутое по частоте на колебательную частоту вещества.
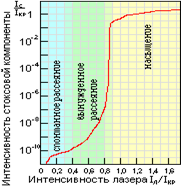
Эксперименты по исследованию влияния интенсивности лазерной накачки на интенсивность стоксовой компоненты показали, что по достижении некоторой критической интенсивности накачки интенсивность стоксовой компоненты резко возрастает, а затем идет насыщение (см. рис.4).
|
|
Макроскопическая теория ВКР. Стоксово рассеяние.
В экспериментах по ВКР было обнаружено, что выходное излучение содержит несколько стоксовых (wл - wu ), (wл - 2wu ), ... и антистоксовых (wл + wu ), (wл + 2wu ), ... компонент. Из рис. 3 видно, что процесс излучения стоксовой компоненты приводит к увеличению населенности колебательного уровня (u=1), поэтому становится возможным излучение на антистоксовой частоте. Стоксова (wc ) и антистоксова (wас ) компоненты могут, в свою очередь, служить исходным излучением, генерирующим частоты wс - wu = wл - 2wu и wас + wu = wл + 2wu . Аналогично можно объяснить появление комбинационных частот более высоких порядков.
Чтобы пояснить основные особенности возникновения ВКР, получим условие усиления или генерации на первой стоксовой частоте wс = wл - wu , т.к. первоначально может усиливаться только эта компонента. Для возникновения других спектральных компонент требуется либо наличие молекул в возбужденном состоянии, либо присутствие стоксовой компоненты первого порядка.
Для анализа используется такая модель: рассеивающая среда состоит из N независимых осцилляторов (т.е. ансамбль осцилляторов не поддерживает волновое движение с отличной от нуля групповой скоростью), каждый характеризуется своим положением z (одномерный случай ¶/¶x=¶/¶y=0) и нормальной колебательной координатой X(z,t). Уравнение движения для осциллятора имеет вид
|
| (1) |
где Г - постоянная затухания, выбранная так, что наблюдаемая ширина линии спонтанного комбинационного рассеяния равна Dn=G /2p ; wu - резонансная частота колебаний молекулы в отсутствие затухания; m - масса; F(z,t) - возбуждающая сила.
Возбуждающую силу можно получить, рассматривая электромагнитную энергию в молекулярной среде. Плотность энергии, запасенной в электрическом поле E=1 /2 eE2 при использовании равенства
|
e = e0 (1 + N a) = e0 {1 + N [ a0 + (¶a/¶X) 0 X]} | (2) |
может быть записана в виде
|
E= 1 / 2 e0 {1 + N [ a0 + (¶a/¶X) 0 X]} E 2 | (3) |
Сила, действующая на единицу объема поляризуемой среды, равна ¶e/¶X, откуда делением на N получаем силу, действующую на один осциллятор.
|
F(z,t)= 1 / 2 e0 (¶a/¶X) 0 <E(z,t)> 2 | (4) |
<E(z,t)> означает усреднение за несколько колебаний, предпринимаемое потому, что молекула неспособна реагировать на эти колебания. Из (4) видно, что при отличной от нуля дифференциальной поляризуемости (¶a/¶X)0 колебания молекул могут возбуждаться электрическим полем.
Дальнейшая задача - показать, как колебания молекул воздействуют на электромагнитное поле. В соответствии с (2) колебания молекул с частотой wu вызывают модуляцию диэлектрической проницаемости с той же частотой. Это приводит к фазовой модуляции поля излучения (появляются боковые составляющие, смещенные на wu друг от друга). Т.е. происходит обмен энергией между электромагнитными полями различных частот., разделенных интервалами, кратными wu .
Полное поле является суммой лазерного (w2 ) и стоксова (w1 ) полей:
|
E(z,t) = 1 / 2 E 1 (z) exp i w1 t + 1 / 2 E 2 (z) exp i w2 t + к.с. | (5) |
|
<E(z,t)> 2 = 1 / 4 E 2 (z) E 1 * (z) exp i( w2 -w1 )t + к .с . | (6) |
|
К-во Просмотров: 897
Бесплатно скачать Реферат: Нелинейная оптика
|