Реферат: Объем фигур вращения правильных многогранников

Тела вращения характеризуются линией, которая при своем вращении относительно оси образует поверхность тела вращения. Эту линию для данного тела вращения называю образующей.

1 . Виды поверхностей в фигурах вращения

Образующими поверхностей вращения в задачах представленных в данной работе служат ребра многогранника, т.е. общие стороны двух граней многогранника.

При вращении любого многогранника вокруг произвольной оси получается тело вращения, которое может быть ограничено только следующими поверхностями:

o плоскостью;

o цилиндрической поверхностью;

o конической поверхностью;

o поверхностью однополостного гиперболоида.

Если прямая (образующая поверхности) перпендикулярна оси вращения, то получается плоскость.

Если прямая (образующая поверхности) параллельна оси вращения, то получается цилиндрическая поверхность.

Если прямая (образующая поверхности) пересекает ось вращения, то получается коническая поверхность.

Если прямая (образующая поверхности) скрещивается с осью вращения, то получается однополостный гиперболоид вращения.

Итак, если прямая (образующая поверхности) скрещивается с осью вращения, то получается однополостный гиперболоид вращения.

Образующими поверхности однополостного гиперболоида в рассматриваемых задачах являются ребра многогранников, лежащие на прямых, скрещивающихся с осью вращения.

2 . Теорема о пересечении гиперболической и цилиндрической поверхностей вращения

Правильные многогранники можно вписать в сферу, поэтому все задачи на вращение правильных многогранников, содержащие пересекающиеся поверхности вращения, удовлетворяют следующей теореме.

Теорема Монжа

Две поверхности второго порядка, которые касаются третьей поверхности второго порядка по плоским кривым линиям, пересекаются между собой по плоским кривым линиям второго порядка.

Очевидно, что в рассматриваемых задачах на вращение правильных многогранников линиями пересечения поверхностей вращения являются окружности.

Как отмечалось, фигуры, полученные в результате вращения многогранника относительно произвольной оси, ограничены лишь такими видами поверхностей как:

o коническая поверхность,

o цилиндрическая поверхность,

o круг или кольцо,

o однополостный гиперболоид.

В задачах 3.2 и 4.2 пересекаются поверхность однополостных гиперболоидов с цилиндрической поверхностью. Образующими этих поверхностей вращения являются ребра многогранников, которые, будучи сторонами правильных многоугольников с нечетным числом сторон, несут в себе интересную закономерность относительно высот каждого вида указанных поверхностей для фигуры вращения.

???????. ???? ?????????? ????????????? ? ???????? ?????? ?????? ????????? ???????????? ???, ???????????? ????? ?? ??? ?????? ? ?????????? ????? ????????????? ? ????????? ?????????????? ? ?????? ???, ?? ?????????? ?? ??? ???????? ????? ??????????? ?????????????? ???????????? ? ?????????????? ???????????, ??????????? ??????? ???????? ??????? ??????????????, ????? ?????????? ?? ??? ???????? ?? ??????? ??????????????, ???????????? ???? ???.

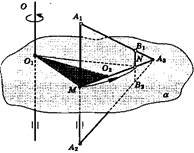3 . Классификация задач на вращение многогранников

Правильный тетраэдр - четырехгранник.

Вычислить объем тела, полученного вращением тетраэдра относительно оси, проходящей через его ребро, если ребро тетраэдра равно a.

Вычислить объем тела, полученного вращением тетраэдра относительно оси, проходящей через центр грани и противоположную вершину, если ребро тетраэдра равно a.