Реферат: Объем фигур вращения правильных многогранников

тогда из ∆А3OK находим

3). .

;

Объем гиперболоида найдем по формуле Симпсона:

Окончательно получаем:

Ответ:

Задача 3.3.

Вычислить объем тела, полученного вращением октаэдра относительно оси, проходящей через центры его противоположных граней, если ребро октаэдра равно а.

Решение:

В данном случае прямые (образующие поверхности) скрещиваются с осью вращения, значит, в результате вращения получается гиперболическая поверхность.

По формуле Симпсона

RВ = RН = R – радиус окружности, описанной около равностороннего треугольника со стороной а (грани октаэдра). Следовательно,

.

Так как перпендикулярным сечением денного тела вращения является окружность, описанная около правильного шестиугольника со стороной (как средняя линия грани октаэдра), то

.

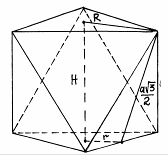Н находим из прямоугольного треугольника по теореме Пифагора:

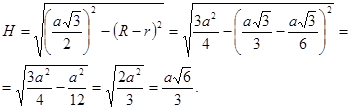
Окончательно получаем:

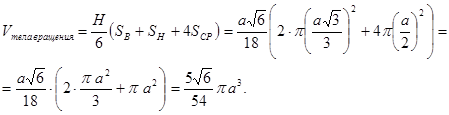
Ответ:

Заключение

Геометрия развивает воображение, говорит о формах окружающего нас мира и помогает познать их красоту. Величайшие художники не могли творить без геометрии.

Удачное, красивое, неожиданное решение геометрических задач всегда приносит радость.

Геометрия представляет большой исторический интерес, имеет серьезное практическое применение и обладает внутренней красотой.