Реферат: Объем фигур вращения правильных многогранников

Куб (или правильный гексаэдр)- шестигранник

Вычислить объем тела, полученного вращением куба относительно оси, проходящей через противоположные вершины, если ребро куба равно a.

Вычислить объем тела, полученного вращением куба относительно оси, проходящей через середины его противоположных ребер, если ребро куба равно a.

Вычислить объем тела, полученного вращением куба относительно оси, проходящей через центры его противоположных граней, если ребро куба равно a.

Октаэдр- восьмигранник

Вычислить объем тела, полученного вращением октаэдра относительно оси, проходящей через противоположные вершины, если ребро октаэдра равно a.

Вычислить объем тела, полученного вращением октаэдра относительно оси, проходящей через середины его противоположных ребер, если ребро октаэдра равно a.

Вычислить объем тела, полученного вращением октаэдра относительно оси, проходящей через центры его противоположных граней, если ребро октаэдра равно a.

4 . Решение задач на вращение многогранников

ТЕТРАЭДР

Задача 1.1.

Вычислить объем тела, полученного вращением тетраэдра

относительно оси, проходящей через его ребро, если ребро тетраэдра равно а.

Решение:

В данном случае прямые (образующие поверхности) пересекают ось вращения, значит, в результате вращения получаются конические поверхности с общим основанием.

;

;

;

;

;

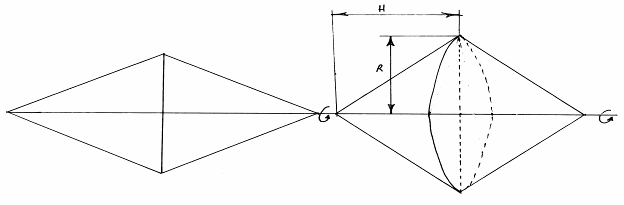
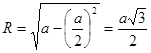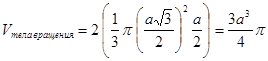Ответ:

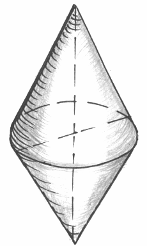Задача 1.2.

Вычислить объем тела, полученного вращением тетраэдра

относительно оси, проходящей через центр грани и противоположную вершину (т.е. через высоту тетраэдра), если ребро тетраэдра равно а.

Решение:

Прямые (образующие поверхности) пересекают ось вращения, значит, в результате вращения получается коническая поверхность.

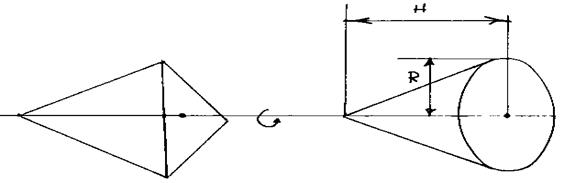
Фигура вращения представляет собой конус, в основании которого находится окружность, описанная около правильного треугольника (грани тетраэдра), а образующие конуса – ребра тетраэдра.

, ??? ;

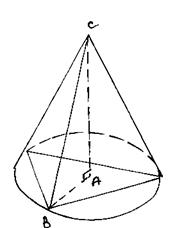Так как основанием тетраэдра является правильный треугольник, следовательно