Реферат: Объем фигур вращения правильных многогранников

.

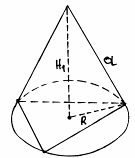1). Для нахождения объема конуса рассмотрим правильную треугольную пирамиду.

Так как основанием пирамиды является равносторонний треугольник со стороной

, то

H1 находим из прямоугольного треугольника, в котором гипотенуза равна а, а один из катетов равен R.

Тогда

.

Таким образом

2). Найдем объем однополостного гиперболоида вращения по формуле Симпсона.

Так как RВ = RН = R, то

Перпендикулярным сечением данного тела вращения является правильный шестиугольник, сторона которого равна половине диагонали грани куба, следовательно, равна

.

Таким образом, RСР является радиусом окружности описанной около правильный шестиугольника со стороной

,

значит

.

Откуда

Так как часть оси вращения, заключенная внутри тела вращения (H) – суть диагональ куба, следовательно,

.

Тогда

Значит,

;

Ответ: