Реферат: Переходные процессы в линейных электрических цепях

Разделив левые и правые части этих соотношений, получим:

Для определения потребного значения емкости примем во внимание, что длительность переходного процесса в спроектированной цепи должно составлять не более

Это означает, что должно выполняться равенство:

5* t =K*t_i или 5*(R₁ +R₂ )*C=K*t_i .

Отсюда получаем потребное значение емкости

Расчет законов изменения напряжений на емкости и резисторах R ₁ , R ₂ в цепи Рис.2.11 можно производить по формулам, приведенным в примере 2.1. Однако, ограничимся расчетом потребных значений R ₁ , C , но выполним электронное моделирование спроектированной цепи.

Результаты расчетов и электронного моделирования приведены в примере 2.5.

Из Рис.2.12, где приведены результаты электронного моделирования, видно, что для спроектированной цепи RC переходной режим является «штатным». Данную цепь можно рассматривать как генератор остроконечных импульсов или преобразователь напряжения: прямоугольные импульсы преобразуются в остроконечные.

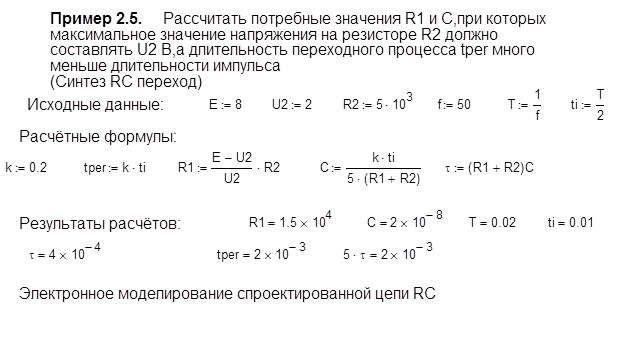
Глава 3. Переходные процессы в цепях второго порядка

3.1 Общая характеристика переходных процессов в цепях второго порядка

Цепями второго порядка называются цепи, в которых содержится два накопителя энергии: индуктивность и емкость.

Электрические цепи второго порядка бывают разветвленными и неразветвленными. К неразветвленным цепям второго порядка относится последовательный колебательный контур. К разветвленным цепям второго порядка относятся Г-образные фильтры нижних и верхних частот.

Электромагнитные процессы в цепях второго порядка описываются дифференциальными уравнениями второго порядка.

Например, дифференциальное уравнение относительно тока в последовательном колебательном контуре можно получить из уравнения, составленного по второму закону Кирхгофа, для мгновенных значений тока и напряжений:

После дифференцирования (3.2) получим дифференциальное уравнение второго порядка относительно тока

Обозначим, как и ранее, искомый ток i ( t ) через Y и разделим левую и правую части (3.3) на L , получим дифференциальное уравнение второго порядка:

где - коэффициент затухания;

- резонансная частота контура;