Реферат: Переходные процессы в линейных электрических цепях
Из курса математики известно, что решение дифференциального уравнения второго порядка, также как и первого, представляется в виде двух слагаемых:
где Y пр ( t ) - принужденная составляющая искомого тока или напряжения, которая зависит от вида источника напряжения, оставшегося в цепи после коммутации;
Y св ( t ) - свободная составляющая, характер которой определяется только структурой цепи образовавшейся после коммутации.
Для решения дифференциального уравнения второго порядка, также как и первого, и по тем же правилам, составляется характеристическое уравнение, которое, в общем, имеет вид:
Корни этого уравнения:
где .
Свободная составляющая искомого тока или напряжения записывается в виде:
(3.8)
где A 1 , A 2 - неизвестные постоянные интегрирования, которые зависят от начальных условий.
Допустим, что для цепи второго порядка составлено характеристическое уравнение (3.6) и определены его корни (3.7), а также найдены принужденные составляющие искомых токов и напряжений. Тогда общее решение дифференциального уравнения можно записать в виде:
. (3.9)
Для определения двух неизвестных 
и 
необходимо составить два уравнения.
В качестве первого уравнения используется уравнение (3.9), а в качестве второго – используется первая производная от (3.9).
Рассматривая (3.9) и (3.10) на момент t =0 , получим два уравнения с двумя неизвестными A 1 и A 2 :
Совместное решение системы (3.11) дает:
После подстановки корней характеристического уравнения (3.6) и найденных постоянных интегрирования (3.12) в формулу общего решения (3.9) и преобразования, получим закон изменения искомого тока или напряжения:
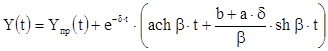
(3.13)
где a = Y (0)- Y пр (0) ; b = Y ’(0)- Y ’пр (0) - постоянные коэффициенты, зависящие от начальных условий.
Отметим, что формула (3.13) является общей для всех токов и напряжений в данной цепи второго порядка. При этом меняются только коэффициенты a и b и их размерность.
При решении конкретных задач могут представиться три случая.
Случай 1 . Корни характеристического уравнения (3.7) действительные и разные, что возможно при d>wk .