Реферат: Переходные процессы в линейных электрических цепях

Из приведенных формул видно, что при подключении цепи RL к источнику синусоидального напряжения ток в переходном режиме содержит две составляющие: синусоиду и экспоненту и его значение, в первый момент после коммутации, зависит от фазы включения.

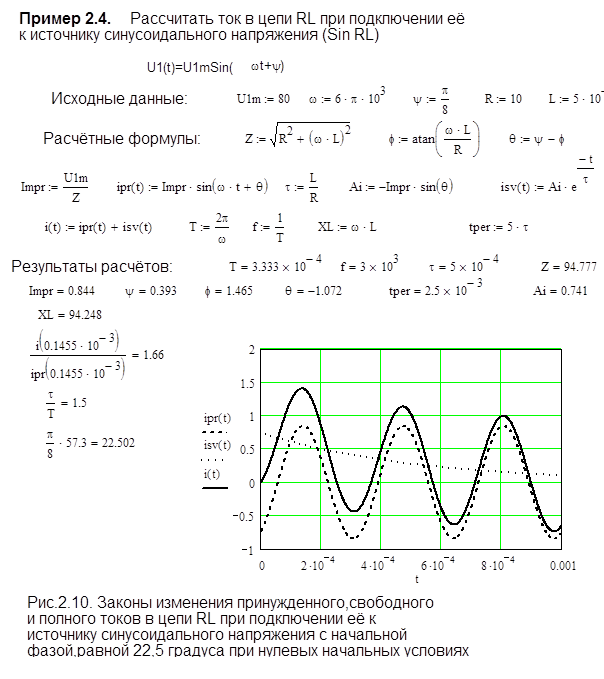
Если включение произошло в момент, когда y = f , то свободная составляющая будет отсутствовать и в цепи сразу будет установившийся режим (удачное включение). Наоборот, неудачное включение имеет место, когда начальная фаза входного напряжения будет y = f ± 90 ° .

Если при этом постоянная времени велика, то в начальный момент после коммутации ток переходного режима может достигнуть почти удвоенной амплитуды принужденной составляющей, что наглядно показано на Рис.2.10, где ток переходного режима в 1,66 раза больше амплитуды принужденной составляющей.

2.6 Синтез цепи RC с заданными параметрами переходного процесса

Выше рассматривались переходные процессы при заданных параметрах RC-элементов.

На практике возникает необходимость в решении обратной задачи: рассчитать потребные значения RC-элементов, при которых обеспечивалась бы заданная длительность переходного процесса и заданное значение выходного напряжения, снимаемого с резистора.

Рассмотрим электрическую цепь, изображенную на Рис.2.11.

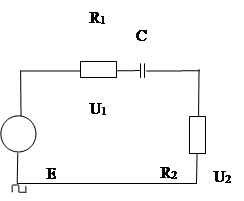Рис. 2.11. Исходная схема для расчета неизвестных R₁ и C

На вход этой цепи подается последовательность однополярных прямоугольных импульсов напряжением E B , длительностью ti , с частотой f и скважностью 2.

Для синхронного управления ключевыми схемами с помощью цепи Рис.2.11 необходимо сформировать остроконечные импульсы, длительность которых была бы во много раз меньше длительности прямоугольных импульсов на входе цепи. Другими словами, заряд и разряд конденсатора должен происходить за время много меньше, чем длительность прямоугольного импульса

где K <<1 - коэффициент длительности переходного процесса в цепи Рис.2.11.

При этом заданными величинами должны быть: сопротивление нагрузки R ₂ , с которого снимается напряжение и максимальное значение U ₂ этого напряжение (U ₂ < E ).

Решение. Из условия задачи следует, что необходимо определить два параметра:

R ₁ - балластное (регулировочное) сопротивление;

C - емкость конденсатора цепи Рис.2.11.

В соответствии с принятым алгоритмом расчета переходных процессов в цепях первого порядка получаем следующее.

1. Независимые начальные условия:

где U ₂ - потребное значение напряжения на нагрузке в момент коммутации.

2. Зависимые начальные условия.

К зависимым начальным условиям, в данном случае, относится напряжение на балластном сопротивление . Для определения этого напряжения составим уравнение по второму закону Кирхгофа и рассмотрим его на момент коммутации (на момент воздействия первого импульса):

На момент воздействия первого импульса t =0 имеем

Поскольку U_C (0)=0, U ₂ (0)= U ₂ , следовательно, U ₁ (0) должно быть равным:

С другой стороны на момент t =0 можно записать