Реферат: Представление численной информации в ЭВМ. Системы счисления

и максимальное:

Очевидно, что диапазон представления чисел в машинах с плавающей запятой значительно больше, чем в машинах с фиксированной запятой:

D= ≈=

Сопоставляя между собой две основные формы представления чисел в ЭВМ, можно прийти к следующим выводам.

Диапазон представления чисел в машинах с фиксированной запятой значительно меньше, чем в машинах с плавающей запятой, а точность зависит от величины исходных чисел. Программирование для машин с фиксированной запятой значительно сложнее, т.к. приходится вводить масштабные коэффициенты, чтобы избежать переполнения масштабной сетки при выполнении арифметических операций.

Однако машины с плавающей запятой конструктивно более сложны, так как необходимо вводить дополнительное оборудование для выполнения операций над порядками чисел, а также предусмотреть операцию нормализации и выравнивания порядков чисел. Время выполнения операций над числами в машине с плавающей запятой больше, чем в машине с фиксированной запятой, что обусловлено необходимостью работы с порядками.

Как и при фиксированной запятой, здесь возможно переполнение разрядной сетки, которое выражается в том, что результат какой-либо операции имеет порядок больше допустимого. Это приводит к аварийной ситуации. При выполнении операций возможно получение чисел, имеющих порядок меньше допустимого и нормализованную мантиссу. Эти числа рассматриваются как машинные нули, так же как и числа, имеющие нулевую мантиссу и допустимый порядок.

Иногда нормальную форму представления чисел называют полулогарифмической, так как порядок числа р выражен в логарифмической форме.

6. Точность представления чисел в ЭВМ

При решении различных задач требуется различная точность получаемых результатов. Так, при решении инженерных задач достаточна точность до 3—4 десятичных знаков (10—13 двоичных), при решении научных задач — 5—6 десятичных или 16—20 двоичных знаков и при решении особо точных задач — до 50 двоичных разрядов.

При ограниченной длине машинных слов множество чисел, которые можно представить в машине, является конечным. Поэтому представление чисел в ЭВМ, как правило, влечет за собой появление погрешностей, величина которых зависит как от формы представления чисел, так и от длины разрядной сетки.

Точность представления числа характеризуется абсолютной и относительной погрешностями.

Абсолютная погрешность — это разность между истинным значением величины А и ее значением, полученным из машинного изображения [А], т. е.

Усредненная абсолютная погрешность представления чисел в машинах с фиксированной запятой определяется как среднее арифметическое между минимально представимым числом и его минимальной потерей, т. е.

В машинах с фиксированной запятой абсолютная погрешность постоянна и равна половине младшего разряда.

Относительная погрешность представления определяется как отношение усредненной абсолютной погрешности к самому числу:

.

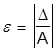Так как само число с фиксированной запятой меняется в пределах

,

то и относительная погрешность является величиной переменной, меняющейся соответственно в пределах

Для машин с фиксированной запятой она определяется следующим образом:

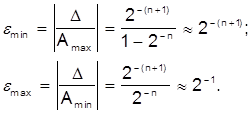
Таким образом, относительная погрешность для машин с фиксированной запятой зависит от величины числа и колеблется в пределах от для больших чисел, до 2^-1 для малых чисел. В машинах с плавающей запятой абсолютная погрешность представления числа определяется следующим образом: