Реферат: Программа государственного экзамена по математике для студентов математического факультета Московского городского педагогического университета

Теорема (основное тождество) . Если x= , то

× .

В частности , если функция qвполне мультипликативна , то и функция также вполне мультипликативна .

Доказательство. Рассмотрим произведение сумм, находящееся в правой части требуемого равенства:

=

==.

Осталось заметить, что для каждого набора (g₁ , g₂ ,..., g_k ) целых неотрицательных чисел g_i , не превосходящих a_i , в сумме

каждое слагаемое встречается ровно один раз. Учитывая теперь, что каждый делитель числа имеет вид , получаем

= .

Свойство полной мультипликативности рассматриваемой функции немедленно вытекает из того, что взаимно простые числа содержат различные простые сомножители. ÿ

3⁰ . Число делителей t ( x ) и сумма делителей s ( x ).

Рассмотрим следующие вполне мультипликативные функции:

t(x )= , где q(x )=1, - число делителей числа x ,

s(x )= , где q(x ) = x , - сумма делителей числа x .

Теорема . Справедливы тождества:

t( )=(a ₁ + 1)( a ₂ + 1)...( a_k + 1),

s( )=.

Доказательство. а) Из определения функции t(x ) немедленно следует указанное тождество, поскольку в силу основного тождества легко подсчитать число слагаемых, каждое из которых равно 1, в каждой из скобок соответствующего произведения.

б) Это тождество получается из основного тождества и формулы суммы членов геометрической прогрессии:

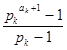.ÿ

4⁰ . Функция Эйлера. Одной из важнейших числовых функций является следующая функция, впервые введенная в рассмотрение Эйлером.

Определение . Через j(x ) обозначается количество чисел ряда

1, 2, ..., x , (*)

взаимно простых с числом x .

Справедлива следующая теорема, которую приведем без доказательства.

Теорема . Если x= , то

j(x )= x ×.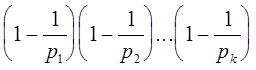

Следствие . Функция Эйлера вполне мультипликативна и

.

Теорема (тождество Гаусса). .

Доказательство. Применяя основное тождество и последнее следствие, получаем, считая ,

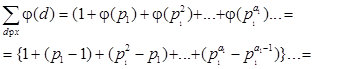
. ÿ

4. Алгоритм Евклида и его применения

1⁰ . Алгоритм Евклида. Наибольший общий делитель чисел a , b можно найти с помощью алгоритма Евклида , который состоит в следующем.

Пусть b >0. Разделим a на b , тогда по теореме о делении с остатком:

a = bq ₁ + r ₁ .

Если r ₁ = 0, то НОД(a , b ) = b .

Если r ₁ ¹ 0, то разделим b с остатком на r ₁ :

b = r ₁ q ₂ + r ₂ .

Если r ₂ = 0, то процесс деления закончим, а если r ₂ ¹ 0, то разделим r ₁ с остатком на r ₂ :

r ₁ = r ₂ q ₃ + r ₃ .

Продолжая далее таким же образом, мы закончим процесс деления кактолько получится остаток равный 0.

Заметим, что такой остаток обязательно получится. В самом деле, остаток всегда меньше делителя,поэтому b > r ₁ > r ₂ > r ₃ > . . . и число получаемых остатков не превосходит b .

Итак, в результате указанного алгоритма получим, что:

a = bq 1 + r 1 ,
b = r 1 q 2 + r 2 ,
r 1 = r 2 q 3 + r 3 ,	(1)
. . . . . . . . . . . . .
rn -2 = rn-1 qn-1 + rn ,
rn-1 = rn qn .