Реферат: Программа государственного экзамена по математике для студентов математического факультета Московского городского педагогического университета
Следовательно, наибольший общий делитель чисел a и b совпадает с последним ненулевым остатком r n в алгоритме Евклида для чисел a и b .
Пример. Найти НОД(160, 72).
Применим к данным числам алгоритм Евклида:
160 = 72×2 + 16, 72 = 16×4 + 8, 16 = 8×2. (2)
Следовательно, НОД(160, 72) = 8.
20 . Теорема (о линейном представлении НОД). Если d - наибольший общий делитель чисел a и b , то существуют такие целые числа x и y , что выполняется равенство : d = xa + yb .
ð Допустим, что числа a и b связаны следующими соотношениями:
| a = bq 1 + r 1 , |
| b = r 1 q 2 + r 2 , |
| r 1 = r 2 q 3 + r 3 , |
| . . . . . . . . . . . . . |
| rn -2 = rn-1 qn-1 + rn . |
Докажем, что каждое из чисел r k линейно выражается через a и b с целыми коэффициентами. Для r 1 утверждение тривиально: r 1 = a - bq 1 . Считая, что каждое из чисел r 1 , r 2 , . . . , rn-1 является целочисленной линейной комбинацией чисел a и b (r k = ak a + bk b ), имеем
rn = an-2 a + bn-2 b - (an-1 a + bn-1 b ) qn-1 = (an-2 - an-1 ) a + (bn-2 - bn-1 qn-1 )b . ð
Пример. Найти линейное представление НОД(160, 72).
Решение. Из второго равенства системы (2) следует, что 8 = 72 - 16×4, а из первого равенства получим, что 16 = 160 - 72×2. Из двух полученных равенств находим: 8 = 72 - 16 × 4 = 72 - (160 - 72 × 2) × 4 = (-4) × 160 + 9 × 72.
Таким образом, искомое представление НОД имеет вид:
8 = (-4) × 160 + 9 × 72.
30 . Связь алгоритма Евклида с непрерывными дробями. Пусть a - рациональная несократимая дробь 
. Для разложения числа a в непрерывную цепную дробь можно воспользоваться алгоритмом Евклида:
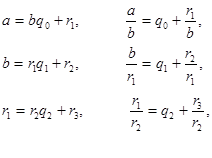
Следовательно,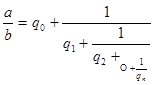 
, откуда
Непрерывные дроби можно использовать для решения различных теоретико-числовых задач.
1. Линейное представление наибольшего общего делителя
Пример 1. Найти линейное представление наибольшего общего делителя чисел (59, 163).
Решение. Разложим в непрерывную дробь число
:
= [2; 1, 3, 4, 1, 2].
Cледовательно, можно теперь заполнить таблицу:
| qs | 2 | 1 | 3 | 4 | 1 | 2 | |
| Ps | 1 | 2 | 3 | 11 | 47 | 58 | 163 |
| Qs | 0 | 1 | 1 | 4 | 17 | 21 | 59 |
| e s | +1 | -1 | +1 | -1 | +1 | -1 |
Отсюда получаем 59 × 58 - 163 × 21 = -1 или 59 × (-58) + 163 × 21 = 1.
2. Решение линейных диофантовых уравнений
Как практически находить какое-нибудь решение линейного неопределенного уравнения
ax + by = c при (a , b )= 1, c= 1 ?
Можно воспользоваться алгоритмом Евклида, из которого легко получить линейное представление НОД чисел a , b ,или представить дробь 
в виде последней подходящей 
, откуда aQn - bPn = (-1)n .
Пример. Решить диофантово уравнение 163x + 59y = 1.
Решение. Мы проверили раньше, что 163 × 21 + 59 × (-58) = 1, следовательно, общее решение имеет вид:
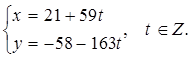
6. Базис и размерность векторного пространства
10 . Линейные комбинации и линейные оболочки векторов. Выражение вида 
= a 1 e 1 + . . . + a n en , где a i - числа, ei - векторы из пространства V, называется линейной комбинацией векторов ei ; числа a i называются коэффициентами линейной комбинации.