Реферат: Программа государственного экзамена по математике для студентов математического факультета Московского городского педагогического университета

(а) Размерность линейной оболочки L(E ) равна рангу системы E (ранг системы - максимальное число ее линейно независимых векторов ): dim L(E ) = r (E ).

(б) Всякая система векторов n-мерного линейного пространства , содержащая более n элементов линейно зависима .

5⁰ . Примеры.

1. Координатное пространство kⁿ имеет стандартный базис из единичных векторов e_i := (0, . . . , 0, 1, 0, . . . , 0) ( единица находится на месте с номером i ), следовательно, dim kⁿ = n . Можно доказать, что система из n векторов-строк образует базис пространства kⁿ Û определитель этой системы отличен от нуля.

2. Базис пространства решений однородной системы линейных уравнений - это фундаментальная система решений.

3. Пространство матриц имеет стандартный базис из матричных единиц E_ij (единица находится на месте с номером (i , j ), следовательно,

dim = nm .

4. Пространства многочленов Q _n [x ] с рациональными коэффициентами степени не превосходящей n имеет следующие базисы:

а) стандартный базис вида 1, x , x ² , . . . , xⁿ ;

б) базис Тейлора “в точке c ”:

1, (x - c ), (x - c )² , . . . , (x - c )ⁿ , где c - некоторое число;

в) [базис Лагранжа “в точке (c ₁ , . . . , c_n+1 )”:

g_i (x ) = {(x - c ₁ ) . . . (x - c_i )^ . . . (x - c_n+1 )}/ {(c_i - c ₁ ) . . . (c_i - c_i )^ . . . (c_i - c_n+1 )},

где c ₁ , . . . , c_n+1 - попарно различные скаляры, а знак ^ означает отсутствие указанного множителя.]

Координаты многочлена f (x )

относительно стандартного базиса - это его коэффициенты;

относительно базиса Тейлора - это строка ;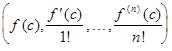

[относительно базиса Лагранжа - это строка (f (c ₁ ), . . . , f (c_n+1 )).]

5. Вещественное линейное пространство C имеет стандартный базис (1, i ).

7. Основные теоремы о системах линейных уравнений

1⁰ . Исследование системы линейных уравнений.

Пусть задана система линейных уравнений: Ax = b , где A - основная матрица, x - столбец переменных, b - столбец свободных членов. С помощью элементарных преобразований строк в основной матрице можно построить максимальную систему единичных столбцов. Кроме того, удалим из расширенной матрицы нулевые строки. Тогда можно считать, что расширенная матрица системы уравнений имеет вид:

,

где в последней строке ведущий элемент обозначен через d .

Для ненулевого числа d возможны два случая:

(а)d находится до черты, т.е. лежит в основной матрице. Следовательно, в этом случае мы можем написать общее решение совместной системы. Заметим, что все переменные будут связаны Û ранг основной матрицы равен числу переменных системы.

(б)d находится после черты; тогда система несовместна и ранг основной матрицы меньше ранга расширенной матрицы на единицу.

Тем самым, мы доказали теорему.

Теорема. Пусть d - ведущий элемент последней строки приведенной ступенчатой матрицы. Тогда

(а) система совместна Ûd находится до черты ;

(б) система несовместна Ûd находится после черты ;

(в) система является определенной Ûd находится до черты и все переменные связанные ;

(г) система является неопределенной Ûd находится до черты и имеется хотя бы одна свободная переменная .

2⁰ . Критерии совместности и определенности .