Реферат: Решение обратной задачи вихретокового контроля
Преобразуем систему уравнений (3.1) с учетом следующих предположений[4] :
-
ОК неподвижен относительно электромагнитного поля т.е. jпер = 0
-
среда изотропна и ее параметры не зависят от напряженностей полей
-
воздействия синусоидальны
-
последовательность дифференцирования по времени и пространственным координатам можно изменять, а операция дифференцирования линейна
-
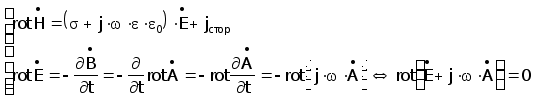
(3.4.1)
(3.4.2)
Поскольку ротор градиента любого скаляра тождественно равен нулю, величину в скобках выражения (3.4.2) можно приравнять градиенту некоторого скаляра y , например скалярного потенциала электрического поля :
-
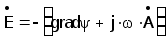
(3.5)
Заменяя векторы напряженности магнитного и электрического поля в (3.4.1) через векторный потенциал магнитного поля получаем :
-
grad div A - DA = -m Чm 0 Ч ( s + jЧwЧeЧe0 ) Ч ( grady + jЧwЧA ) + m Чm 0 Чjстор
(3.6)
Откуда после очевидных преобразований следует:
-
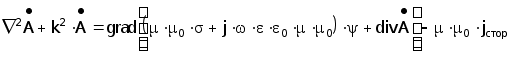
(3.7)
где
-
k2 = w2 Ч m Ч m 0 Ч e Ч e0 - j Ч w Ч m Ч m 0 Ч s
(3.8)
Поскольку векторный потенциал магнитного поля задан с точностью до градиента некоторого скаляра, а потенциал y с точностью до постоянной величины, имеется возможность положить значение величины в квадратных скобках выражения (3.7) равное нулю (так называемая калибровка Лоренца). В результате получаем уравнение Гельмгольца для векторного потенциала магнитного поля :
-
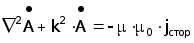
(3.9)
В дальнейших рассуждениях используем следующие предположения :
-
Поле НВТП квазистационарно в том смысле, что волновыми процессами в воздухе можно пренебречь. Это вполне оправдано т.к. размеры НВТП и ОК обычно много меньше длины волны в воздухе, а потери на излучение по сравнению с потерями в ОК малы.
-
В проводящем теле будем рассматривать только волновые процессы, обусловленные наличием параметров s и m т.е. токами смещения( пропорциональными wЧeЧe0 ) как и в воздухе пренебрегаем. Легко показать, что это предположение справедливо не только для металлов, но и для полупроводниковых материалов с удельным сопротивлением r до 50[ОмЧсм]. В этом случае выражение (3.8) принимает вид :
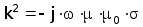 .
.
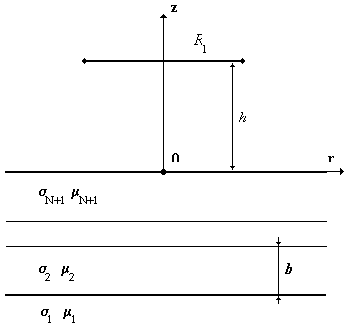
3.2 Поле витка над многослойной средой