Реферат: Решение обратной задачи вихретокового контроля

( 2.4.13)

Отметим основное преимущество такого решения. Несмотря на определенную сложность вычислений при решении интегральных уравнений (2.4.2-2.4.8) для расчета градиента импеданса НВТП необходимо решить только две такие задачи.

2.4.2 Отечественные методы решения

Подход, в значительной мере аналогичный работам [45-51] был предложен в работе [41]. Из-за небольшого объема в ней уделено недостсточное внимание вопросам практической реализации, объяснены не все обозначения и не приведены результаты численного моделирования. В целом это значительно снижает практическую ценность статьи. Приведем основные положения этой работы.

Прямая задача

Пусть круговой виток радиусом а с током I находится в точке P=P_s(r,j,z), jО(-p,p) вблизи немагнитного ОК, занимающего область V. Пусть ОК обладает электрической проводимостью s=s₀Чs(Р) являющейся произвольной функцией координат. Требуется по N измерениям величины э.д.с. определить s как функцию координат точек PОV. Причем i-ое измерение э.д.с. будем проводить на i-ом измерительном круговом витке с координатами P_i=P_i(r,j,z) i=1,N при неизменных частоте и расположении возбуждающего витка.

В общем случае напряженность электрического поля Е определяется через векторный магнитный потенциал А, причем А = А₀ + А_вн, где А₀ - возбуждающий, а А_вн - вносимый потенциалы.

(2.4.14)

Вводя функцию Грина G(p,p₀) получим

(2.4.15)

При этом вносимая напряженность электрического поля

Eвн = -jЧwЧAвн

(2.4.16)

Вносимая э.д.с., наводимая в i-ом витке

(2.4.17)

где функция Грина G(P,P₀) имеет вид

(2.4.18)

В дальнейшем рассмотрим случай, при котором V-полупространство (r>0,\j\<p,z<0) с электрической проводимостью s=s₀Чs(Р), где s(Р) - произвольная функция координаты z. В этом случае выражение (2.4.17) примет вид

(2.4.19)

где k²=jwm₀s₀ .

Для напряженности электрического поля Е(Р) справедливо представление

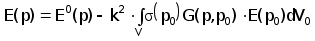
(2.4.20)