Реферат: Решение обратной задачи вихретокового контроля
После проведения серии из N измерений величины eвн выражение (2.4.19) дает связь между вносимыми ЭДС ei и s(z)E(r,z). Чтобы определить непосредственно s=s(z), находим E(r,z) при известной функции s(z)E(r,z) из (2.4.20), после чего исключаем E(r,z) из известного.
Обозначим x(p)=-k2s(z)E(r,z), а измеряемую совокупность ЭДС через Fi. Тогда (2.4.19) можно записать в операторной форме как
-
F = Px + d
(2.4.21)
где d - погрешность измерения.
Обратная задача
Построим функционал Ф(х)=||F-Px||2+a||x-x0||2, где х0 - некоторое известное ІблизкоеІ к искомому распределение, удовлетворяющее F0=Px0. Образуем вариацию функционала Ф(х), используя определение сопряженного оператора (Px,y)=(x,P*y). Для нахождения минимума Ф(х) приравняем его вариацию dФ нулю.
Вводя вспомогательную функцию u=x-x0 и учитывая F0=Px0 проведем ряд преобразований. Искомое распределение s(z) можно найти из равенства
-
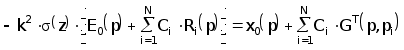
(2.4.22)
где напряженность электрического поля в точке р для известного распределения s(z) имеет вид
-
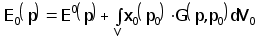
(2.4.23)
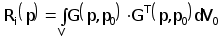
(2.4.24)
Система алгебраических уравнений для определения коэффициентов Сi имеет вид
-
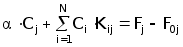
(2.4.25)
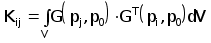, j=1,N(2.4.26)
3. Прямая задача ВТК для НВТП
3.1 Уравнение Гельмгольца для векторного потенциала
Взаимодействие преобразователя с объектом контроля определяется системой уравнений Максвелла в дифференциальной форме[6] :
-
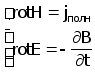
(3.1)
где