Реферат: Решение обратной задачи вихретокового контроля
- ток, протекающий по нитевидной возбуждающей обмотке с радиусом R1, находящейся на расстоянии h от N-слойной среды
jстор = I Ч d( z - h ) Ч d(r - R1)
Отметим, что в силу осевой симметрии системы
В цилиндрической системе координат выражение (3.9) имеет следующий вид :
-
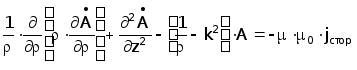
(3.10)
Применяя к (3.10) преобразование Фурье-Бесселя с ядром в виде функции Бесселя первого порядка имеющее вид :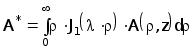
получаем
-
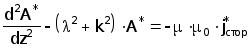
(3.11)
Так как на поверхностях раздела слоев ОК должна сохранятся непрерывность тангенциальных составляющих векторов напряженностей магнитного и электрического поля, дополняем уравнение (3.11) граничными условиями на поверхностях слоев ОК( граничные условия одинаковы для А и А* ) :
-
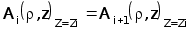
(3.12)
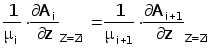
(3.13)
Решив уравнение (3.11) с учетом граничных условий (3.12-3.13) и применяя к решению обратное преобразование Фурье-Бесселя имеющее вид : 
получаем для полупространства над ОК
|
|
(3.14) |
где j=j( l , m , s ) - функция граничных условий.
3.3 Воздействие проводящего ОК на НВТП
Для большинства инженерных расчетов можно использовать нитевидную модель обмоток НВТП использованную в (п 3.2). При данном упрощении получаем :
-
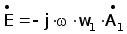
- напряженность электрического поля
(3.15)
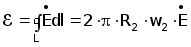
- ЭДС наводимая в измерительной обмотке с радиусом R2 и числом витков w2
(3.16)
Анализируя формулу (3.14) можно заметить, что первый интеграл представляет собой векторный потенциал создаваемый возбуждающей обмоткой, а второй интеграл - векторный потенциал вносимый ОК. В практике ВТК обычно анализируются вносимые параметры НВТП (напряжение, импеданс) поэтому получим выражение для вычисления вносимого напряжение кругового трансформаторного накладного ВТП используя (3.15-3.16):
-
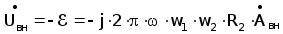
(3.17)