Реферат: Розробка учбового матеріалу для викладання вищої математики на тему "Наближені методи обчислення визначених інтегралів"
В загальному вигляді задача чисельного інтегрування може бути викладена наступним чином [1]. Нехай інтеграл, який потрібно визначити, представлено у вигляді
 (1.3)
(1.3)
Підінтегральна функція в формулі (1.3) є такою, що не дозволяє в функціональному вигляді отримати первісну функцію.
Цей інтеграл обчислюємо за наближеною квадратурною формулою:
 (1.4)
(1.4)
де: функція ![]() - визначена і неперервна на інтервалі
- визначена і неперервна на інтервалі ![]() ;
;
![]() - вагова функція, яка може мати якісь особливості на відрізку
- вагова функція, яка може мати якісь особливості на відрізку
інтегрування, наприклад, перетворюватись у нескінченість в
деяких точках цього відрізка.
![]() - квадратурні коефіцієнти;
- квадратурні коефіцієнти;
![]() - квадратурні вузли (
- квадратурні вузли (![]() );
);
n - довільне число інтервалів всередині відрізку [a,b].
Сума, що стоїть у правій частині наближеної рівності (1.4), називається квадратурною сумою.
Параметри ![]() ,
,![]() вибирають так, щоб або похибка квадратурної формули була по можливості мінімальною, або обчислення за формулою (1.4) були достатньо простими. Різні квадратурні формули відрізняються одна від одної способами вибору параметрів
вибирають так, щоб або похибка квадратурної формули була по можливості мінімальною, або обчислення за формулою (1.4) були достатньо простими. Різні квадратурні формули відрізняються одна від одної способами вибору параметрів ![]() ,
,![]() .
.
Більшість квадратурних формул базується на заміні підінтегральної функції ![]() алгебраїчними багаточленами різного степеня.
алгебраїчними багаточленами різного степеня.
Означення: Кажуть, що квадратурна формула (1.4) має алгебраїчний степінь точності ![]() , якщо ця наближена формула стає точною на множині всіх алгебраїчних багаточленів не вище
, якщо ця наближена формула стає точною на множині всіх алгебраїчних багаточленів не вище ![]() -ого степеня.
-ого степеня.
Це означає, що якщо до наближеної формули (1.4) замість функції ![]() підставити будь-який алгебраїчний багаточлен
підставити будь-який алгебраїчний багаточлен ![]() -ого степеня, то наближена рівність (1.4) стає точною, тобто
-ого степеня, то наближена рівність (1.4) стає точною, тобто
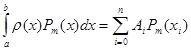
![]() (1.5)
(1.5)
Але при цьому наближена рівність (1.4) не для всіх багаточленів степеня ![]() буде точною.
буде точною.
Алгебраїчний степінь точності квадратурної формули є мірою точності цієї формули. Оскільки будь-яку неперервну функцію ![]() можна як завгодно точно наблизити алгебраїчними багаточленами (за рахунок збільшення степеня багаточлена), то слід очікувати, що квадратурні формули, які мають високий алгебраїчний ступінь точності, будуть мати високу точність для будь-яких неперервних функцій
можна як завгодно точно наблизити алгебраїчними багаточленами (за рахунок збільшення степеня багаточлена), то слід очікувати, що квадратурні формули, які мають високий алгебраїчний ступінь точності, будуть мати високу точність для будь-яких неперервних функцій ![]() .
.
Параметри ![]() ,
,![]() можна вибрати так. щоб зробити алгебраїчний ступінь точності квадратурної формули якомога вищим. Такі формули називаються квадратурними формулами найвищого степеня точності. Вперше вони були розглянуті Гауссом і тому їх часто називають формулами гауссового типу.
можна вибрати так. щоб зробити алгебраїчний ступінь точності квадратурної формули якомога вищим. Такі формули називаються квадратурними формулами найвищого степеня точності. Вперше вони були розглянуті Гауссом і тому їх часто називають формулами гауссового типу.
Якщо вузли ![]() вибрати з міркувань зручності (рівномірно розташованими
вибрати з міркувань зручності (рівномірно розташованими ![]() ,), а коефіцієнти
,), а коефіцієнти ![]() - з міркувань точності, то у випадку
- з міркувань точності, то у випадку ![]() отримаємо квадратурні формули Ньютона - Котеса [2].
отримаємо квадратурні формули Ньютона - Котеса [2].
Якщо вузли ![]() вибрати з міркувань точності, а коефіцієнти
вибрати з міркувань точності, а коефіцієнти ![]() - з міркувань зручності (всі коефіцієнти однакові), то добудемо квадратурні формули, що носять ім’я Чебишова [2].
- з міркувань зручності (всі коефіцієнти однакові), то добудемо квадратурні формули, що носять ім’я Чебишова [2].
Обгрунтування інтерполяційних квадратурних формул будується на наступних висновках [1].
Нехай на відрізку інтегрування якось зафіксовані різні між собою вузли ![]() , і будемо вибирати лише коефіцієнти
, і будемо вибирати лише коефіцієнти ![]() (
(![]() ) так, щоб формула (1.4) була якомога точнішою. Припускаємо,
) так, щоб формула (1.4) була якомога точнішою. Припускаємо, ![]() , тобто функія
, тобто функія ![]() і всі її похідні до
і всі її похідні до ![]() порядку включно є неперервними на відрізку
порядку включно є неперервними на відрізку ![]() . Візьмемо квадратурні вузли як вузли інтерполяції (оскільки вони всі з відрізку інтегрування та всі різні між собою), та побудуємо інтерполяційний багаточлен
. Візьмемо квадратурні вузли як вузли інтерполяції (оскільки вони всі з відрізку інтегрування та всі різні між собою), та побудуємо інтерполяційний багаточлен ![]() для функції
для функції ![]() . Будемо мати таку рівність
. Будемо мати таку рівність
![]() (1.5)
(1.5)
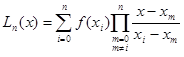 (1.6)
(1.6)
![]() (1.7)
(1.7)
![]() (1.8)
(1.8)