Реферат: Розробка учбового матеріалу для викладання вищої математики на тему "Наближені методи обчислення визначених інтегралів"

Геометричне зображення „формули правих прямокутників" наведене на рисунку (2.3).

Рис.2.3 Геометричне зображення „формули правих прямокутників”

3. Узагальнена квадратурна формула „центральних прямокутників" запишеться у вигляді:

(2.1 20)

її залишок має вигляд

(2.1 21)

Геометричне зображення „формули центральних прямокутників" наведене на рисунку (2.4).

Рис.2.4 Геометричне зображення „формули центральних прямокутників"

2.2 Метод трапецій

Квадратурна „формула трапеції” - це виключний випадок формули Н’ютона - Котеса (1.20), коли [1]. Квадратурна формула трапеції має вигляд:

(2.2.1)

Два коефіцієнти Котеса знаходимо, враховуючи їхні властивості

Тоді формула трапеції має вигляд

(2.2.2)

Геометричне тлумачення наведене на рис.2.5 Геометрично цю формулу отримаємо, якщо криву замінити хордою, яка проходить через точки та , тоді інтеграл знаходиться як площа трапеції .

Рис.2.5 Геометричне тлумачення „формули трапецій”

Формула (2.2.2) наближена. Визначимо похибку для квадратурної формули трапеції:

Похибка квадратурної формули (2.2.2) випливає з (1.12), якщо взяти та

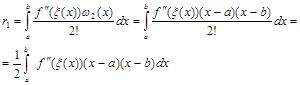
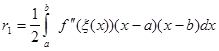(2.2.3)

До обчислення останнього інтеграла застосуємо теорему про середнє [5].

Теорема. Нехай - інтегровані на проміжку функції, причому , на всьому проміжку не змінює знак. Тоді

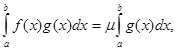де

Якщо неперервна на , то ця формула може бути записана у вигляді

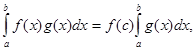де