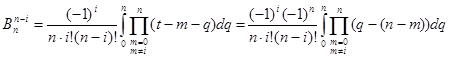Реферат: Розробка учбового матеріалу для викладання вищої математики на тему "Наближені методи обчислення визначених інтегралів"

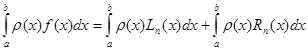(1.9)

підставимо (1.6), (1.7), (1,8) до формули (1.9)

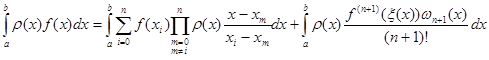(1.10)

Якщо позначити

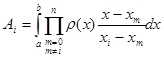(1.11)

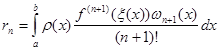(1.12)

то інтеграл (1.10) можна переписати у вигляді

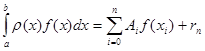( 1.13)

Відкинувши у (1.13) похибку , добудемо наближену формулу (1.4).

Означення. Квадратурна формула (1.4) будемо називати інтерполяційною, якщо квадратурні коефіцієнти , визначаються формулами (1.11). Нагадаємо, що квадратурні вузли при цьому всі різні та всі розташовані на відрізку інтегрування, в усьому іншому вони довільні.

Формула (1.12) визначає похибку інтерполяційної квадратурної формули. З похибки видно, що алгебраїчний степінь точності інтерполяційної квадратурної формули дорівнює . Збільшити степінь точності можна лише за рахунок вибору вузлів .

Квадратурні формули при сталій ваговій функції та з рівновіддаленими вузлами називають формулами Ньютона-Котеса у пам’ять того, що вперше вони в достатньому загальному вигляді були розглянуті Ньютоном, коефіцієнти вперше були добуті Котесом [4].

Кінечний відрізок інтегрування ділимо на рівних частин довжини , точки ділення беремо за вузли інтерполяційної формули. Спростимо вигляд квадратурних коефіцієнтів ,, які визначаються формулою (1.11), підставивши туди

,.

Крім того перейдемо до нової змінної інтегрування , де

Для виконання всіх цих дій спочатку розглянемо добуток у формулі (1.11)

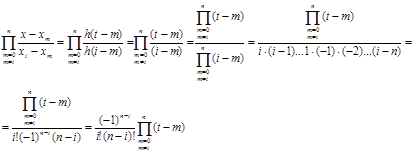(1.14)

Підставимо добуток (1.14) до формули (1.11) та перейдемо до нової змінної, будемо мати

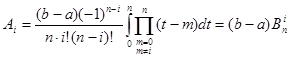(1.15)

Де

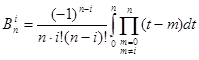(1.16)

Квадратурна формула Ньютона-Котеса приймає вигляд

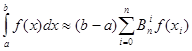(1.17)

Алгебраїчна степінь точності формули (1.17) дорівнює . Коефіцієнти (1.16) називаються коефіцієнтами Котеса. Вони мають властивості:

. Дійсно, підставимо до формули (1.17) , тоді , при цьому наближена формула стає точною. Виконуємо інтегрування властивість доведена.

, тобто рівновіддалені від кінців коефіцієнти формули Ньютона -Котеса є однаковими. Дійсно, маємо з формули (1.16)

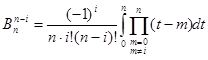
Зробимо заміну змінної інтегрування тоді