Реферат: Розробка учбового матеріалу для викладання вищої математики на тему "Наближені методи обчислення визначених інтегралів"

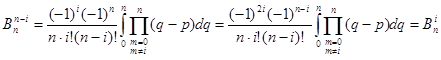
3. Коефіцієнти не залежать від довжини відрізка інтегрування та підінтегральної функції, тому вони можуть бути обчислені раз і назавжди

В залежності від вибраного параметра n отримана загальна форма квадратурних рівнянь розподіляється на випадки [6]:

1) Коли , то застосовуєма форма квадратурних рівнянь називається - „квадратурна формула трапеції”;

2) Коли , то застосовуєма форма квадратурних рівнянь називається - „квадратурна формула Симпсона”;

3) Коли , формула (1.19) не застосовується, оскільки значення не визначені, тому застосовується особливий випадок „квадратурної формули прямокутників (ліві, праві, центральні) ".

2. Чисельні методи інтегрування

2.1 Метод прямокутників

Нехай є відрізок і нам треба обчислити визначений інтеграл

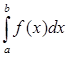⁽ 2.1 1)

за попередньо представленою загальною квадратурною формулою Н’ютона - Котеса (1.4)

⁽ 2.1 2)

де - деякі фіксовані вузли

Найпростіший варіант інтерполяційної квадратурної формули (2.1 2) виникає, коли [1]. У цьому випадку не можна скористатися формулою (1.20), бо коефіцієнт (1.19) при невизначений. Тому, як і при побудові загальної інтерполяційної формули, замінимо підінтегральну функцію інтерполяційним багаточленом нульового степеня, що побудований за єдиним вузлом .

(2.1 3)

при заміні підінтегральної функції (2.1 2) інтерполяційним поліномом нульового степеня, що побудований по єдиному вузлу

⁽ 2.1 3)

Знайдемо коефіціент

(2.1 4)

Після інтегрування маємо квадратурну „формулу прямокутника”:

, (2.1 5)

При її називають формулою лівих прямокутників,

При її називають формулою правих прямокутників,

При - центральних (або середніх) прямокутників.

Геометричне тлумачення цієї формули показано на рис 2.1

Рис.2.1 Геометричне зображення „формули прямокутників"

Оцінимо похибку квадратурної формули (2.1 5) за умови, що . За означенням похибки квадратурної формули (2.1 5) маємо

(2.1 6)

Функцію запишемо у вигляді розвинення в ряд Тейлора в околі точки [7]:

(2.1 7)