Реферат: Шпоры по вышке

1. Матрицы. Линейные операции над ними и их свойства.

Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины.

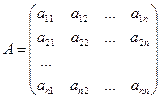
Матрицы равны между собой, если равны все их соответствующие элементы.

Матрица, у которой число строк и столбцов равно – называется квадратной .

Матрица, все элементы которой, кроме элементов главной диагонали равны нулю, называется диагональной .

Диагональная матрица, у которой все элементы главной диагонали равны 1, называется единичной . Обозначается буквой Е.

Матрица, у которой все элементы по одну сторону от главной диагонали равны нулю, называется треугольной .

Матрица, у которой все элементы равны нулю, называется нулевой .

1.

2.

3.

4.

5.

6.

7.

8.

2. Умножение матриц. Транспонирование. Свойства.

Операция умножения возможна, если количество столбцов первой матрицы равно количеству строк другой матрицы.

где

1.

2.

3.

4.

Матрица, полученная заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной , к данной.

1.

2.

3. Определители матриц. Свойства определителей. Миноры и алгебраические дополнения.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--