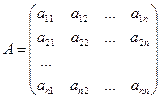Реферат: Шпоры по вышке

2. Смешанное произведение не изменится при перемене местами векторного и скалярного произведения.

3. Смешанное произведение меняет знак при перемене мест любых двух векторов-сомножителей.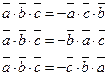

4. Смешанное произведение трех ненулевых векторов равно нулю тогда и только тогда, когда они компланарны.

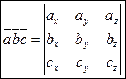
Три вектора называются компланарными, если результат смешанного произведения равен нулю.

16. Линейные преобразования пространства. Матрица линейного преобразования. Связь между координатами образа и прообраза.

Рассмотрим линейное пространство V, в котором каждому элементу x, в силу некоторого закона поставлен элемент этого же пространства.

- прообраз

- образ

Каждому прообразу соответствует единственный образ.

Каждый образ имеет единственный прообраз.

Линейное преобразование пространства, при котором существует взаимнооднозначные соответствия.

Блективное преобразование – называется линейным, если выполняются 2 условия.

1.

2.

Рассмотрим n-мерное линейное пространство

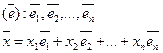
Для того, чтобы задать линейные преобразования в этом пространстве достаточно задать это преобразование для базисных векторов.

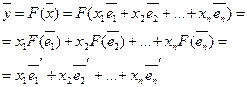
Матрица линейного преобразования.

Пусть F – линейное преобразование линейного пространства, переводящая базис в базис . Т.к. - базис, то верны соотношения
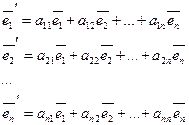