Реферат: Шпоры по вышке

26. Поверхности вращения.

Поверхность, образованная вращением некоторой плоской кривой вокруг оси, лежащей в ее плоскости, называется поверхностью вращения. Пусть некоторая кривая L лежит в плоскости Oyz. Уравнение этой кривой запишутся в виде:

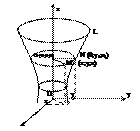Найдем уравнение поверхности, образованной вращением кривой L вокруг оси Oz.

Возьмем на поверхности точку

M (x;y;z). Проведем через точку

М плоскость, перпендикулярную

оси oz, и обозначим точки

пересечения ее с осью oz

и кривой Lсоответственно O₁ и N.

Обозначим координаты точки

N (0;y₁ ;z₁ ). Отрезки O₁ Mи O₁ N

являются радиусами одной и той же окружности. Поэтому O₁ M= O₁ N. Но O₁ M = (x² +y² )^0.5 , O₁ N=|y₁ |.

Следовательно, |y₁ |=(x² +y² )^0.5 или y₁ =±(x² +y² )^0.5 . Кроме того, очевидно, z₁ =z.

Следовательно – искомое уравнение поверхности вращения, ему удовлетворяют координаты любой точка М этой поверхности и не удовлетворяет координаты точек, не лежащих на поверхности вращения.

27. Поверхности 2-го порядка. Эллипсоид, Гиперболоид.

Эллипсоид.

Рассмотрим сечение поверхности с плоскостями, параллельными xOy. Уравнения таких плоскостей z=h, где h – любое число. Линия, получаемая в сечении, определяется двумя уравнениями:

Если |h|>c, c>0, то точек пересечения поверхности с плоскостями z=h нет.

Если |h|=c, т.е. h=±c, то . Линия пересечения вырождается в две точки (0;0;с) и (0;0;-с). Плоскости z=c и z=–cкасаются поверхности.

Если |h|<c, то уравнения можно переписать в виде: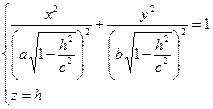

Линия пересечения есть эллипс с полуосями.

Эллипсоид – замкнутая овальная поверхность, где a,b,с – полуоси. Если все они различны, то эллипсоид называется трехосным . Если какие-либо две полуоси равны, то тело называется эллипсоид вращения, если a=b=c, то тело называется сферой x² +y² +z² =R²

Однополостный гиперболоид.

Пересекая поверхность плоскостью z=h, получим линию пересечения, уравнения которой имеют вид.